قانون طول المستطيل

قانون طول المستطيل نتحدث عنه من خلال مقالنا هذا كما نذكر لكم مجموعة متنوعة أخرى من الفقرات عن المستطيل مثل قانون حساب محيط المستطيل ومفهوم المستطيل والختام معلومات عن مادة الرياضيات.

قانون طول المستطيل

هناك العديد من القوانين التي يمكن استخدامها لحساب طول قطر المستطيل ومنها ما يلي:
1-عند معرفة أحد أبعاد المستطيل ومحيطه:
من الممكن حساب طول قطر المستطيل كالآتي:
طول قطر المستطيل = الجذر التربيعي للناتج من (مربع المحيط -٤×المحيط× الطول أو العرض+٨× مربع الطول أو العرض)/٢.
القانون بالرموز: ق= (ح²-٤×ح× أ+٨× أ²)√/٢
ق=(ح²-٤×ح ×ب +٨× ب²)√/٢ تشير الرموز إلى:
ق: قطر المستطيل.
أ: طول المستطيل.
ب: عرض المستطيل.
ح: محيط المستطيل.
2-عند معرفة الزاوية التي تجاور القطر والضلع المقابل لها:
من الممكن حساب طول القطر بمعرفة قيمة الزاوية المحصورة بين القطر وبين الضلع المجاور للقطر والضلع الذي يقابله.
يمكن استعمال القوانين التالية في حساب طول القطر:
طول قطر المستطيل= الضلع المقابل للزاوية التي تجاور القطر/ جا(الزاوية التي تجاور القطر).
شاهد ايضا جدول الضرب كامل
القانون بالرموز:
ق= أ/ جا(α).
3-عند معرفة أحد أبعاد المستطيل ومساحته:
يمكن حساب طول القطر من القانون طول قطر المستطيل = الجذر التربيعي للقيمة (مربع المساحة + أحد الأبعاد (الطول أو العرض)4) /الطول أو العرض.
الرموز: ق= (م²+أ4)√/أ، أو ق= (م²+ب4)√/ب.
تشير الرموز إلى:
ق: قطر المستطيل.
أ: طول المستطيل.
ب: عرض المستطيل.
م: مساحة المستطيل.
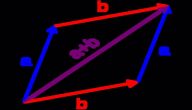
4- عند معرفة طول وعرض المستطيل:
يعمل القطران على تقسيم المستطيل إلى مثلثيْن متطابقين بهما زاوية قائمة.
في كل مثلث يكون القطر هر الوتر.
تبعاً لـ نظرية فيثاغورس يمكن حساب طول قطر المستطيل كالآتي:
طول قطر المستطيل = الجذر التربيعي للناتج من (الطول²+العرض²).
الرموز: ق=(أ²+ب²)√.
تشير الرموز إلى:
ق: قطر المستطيل.
أ: طول المستطيل.
ب: عرض المستطيل.

قانون حساب محيط المستطيل

من الممكن أن نستطيع حسابة محيط المستطيل بالكثير من الطرق ومنها:
1-عندما تكون علي علم بالطول والقطر، أو طول القطر والعرض: محيط المستطيل= 2× (الطول أو العرض+ (مربع القطر-مربع الطول أو مربع -العرض) √)، وبالرموز: ح= 2×(أ+(ق²-أ²) √)، أو ح= 2×(ب+(ق²-ب²) √)؛ حيث:
أ: طول قطر المستطيل.
ب: محيط المستطيل.
ح: عرض المستطيل.
ق: طول المستطيل.
2-عندما تكون علي علم بطوله وعرضه يكون محيط المستطيل=طول الضلع الأول+ طول الضلع الثاني+ طول الضلع الثالث+ طول الضلع الرابع،وذلك بسبب أن كل ضلعين متساويان بالنسبة للمستطيل متساويان في الطول، فمن الممكن أن يكتب القانون بهذا الشكل: محيط المستطيل= 2×الطول+2×العرض، وبالرموز: ح=2×أ+2×ب، حيث:
أ: عرض المستطيل.
ب: طول المستطيل.
3-عندما تكون علي علم بالطول والعرض، أو الطول والمساحة يكون محيط المستطيل= (2×مساحة المستطيل+2×مربع الطول أو مربع العرض) /الطول أو العرض، وبالرموز: ح=((2×م+2×أ²) /أ أو ح=((2×م+2×ب²) /ب؛ حيث:
أ: عرض المستطيل.
ب: طول المستطيل.
ح: مساحة المستطيل.
م: محيط المستطيل.

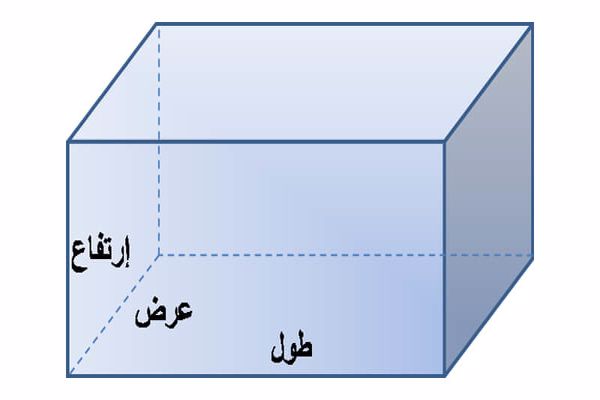
مفهوم المستطيل

المستطيل هو بادئ ذي بدء الشكل المسطح الهندسي وهو يتألف من أربع نقاط مترابطة من قبل اثنين من أزواج من قطاعات متساوية ، تتقاطع بشكل عمودي فقط في هذه النقاط ويتم تعريف المستطيل من خلال متوازي الاضلاع. بطريقة أخرى ، المستطيل عبارة عن رسم متوازي ، وكلها زوايا مستقيمة ، أي تساوي 90 درجة وفي هندسة الإقليدية ، إذا كان الشكل الهندسي له 3 من 4 زوايا تساوي 90 درجة ، فإن الزاوية الرابعة تكون تلقائيًا 90 درجة ويمكن تسمية هذا الشكل مستطيلًا. من تعريف متوازي الاضلاع ، من الواضح أن المستطيل هو العديد من أنواع هذا الرقم على المستوى. ويترتب على ذلك أن خصائص متوازي الاضلاع قابلة للتطبيق على المستطيل. على سبيل المثال: في المستطيل ، تكون الأطراف المقابلة متساوية في الطول.
خصائص المستطيل:
1-يتم حساب حجم المستطيل اما بجمع أطوال أضلاعه او بضرب مجموع الطول بالعرض في الرقم 2.
2-المستطيل هو شكل متوازي اي ان اي ضلعين متقابلين متوازيين لا يلتقيان وتكون الزاوية بينهما 180 اما الأضلاع التي تحتوي على رؤوس مشتركة تكون الزاوية بينها 90
3-ان تساوت أضلاع المستطيل اي تساوى الطول بالعرض يكون الشكل مربع
4-المستطيل شكل ثنائي الأبعاد يتكون من طول وعرض ويتم حساب مساحته عن طريق ضرب طوله بعرضه ويكون الناتج وحدة مساحة مربعة

معلومات عن مادة الرياضيات

-مادة الرياضيات اكتشفت منذ قديم الزمان أي منذ نشأة الإنسان، لذلك ليس لها تعريف موحد لأن كل عصر يقوم بالتطوير من علوم الرياضيات وإضافة أشياء جديدة على التعريف، فأرسطو كان يطلق عليه علم الكميات. يقصد به قدرة الإنسان على عد الأشياء، ومعرفة كمياتها، وهذا أمر بديهي لدى الإنسان أي يوجد في فطرته مع تعلم بسيط، ثم تطورت الرياضيات في عصر السامرين والبابليين والفراعنة.
حيث أثبتت الدراسات أنهم كانوا يستخدمون علم القياس والجبر وعلم الفلك والعلوم المالية والبناء، أي يستخدمون الرياضيات في أغلب الجوانب الحياتية.
-ومن ثم انتشرت العلوم الرياضية وأخذت ذروتها في العصور الإسلامية، علم الرياضيات من العلوم التي ترتبط ارتباط وثيق بعلوم أخرى مثل علم الفيزياء والكيمياء وعلم الأحياء البيولوجيا ومن فروع الرياضيات؛ التفاضل والتكامل والهندسة الرياضية ونظرية الأعداد والجبر ومعادلات تفاضلية وطوبولوجيا.
-فالرياضيات يستخدمونها لإثبات الحقيقة عن طريق تخمين دقيق للأشياء والتعاريف المختارة بشكل مناسب. عرف الرياضي الفرنسي أوزانا سنة 1691، الرياضيات هي العلم الذي يدرس كل ما يمكن قياسه أو حسابه، وتم تدريس الرياضيات في كافة المراحل التعليمية سواء في المدرسة الابتدائية أو الإعدادية والثانوية. كذلك الجامعات ولها تخصصات عامة بها في الكلية، وذلك لاهتمامها وارتباطها الوثيق بحياتنا اليومية.