قانون مساحة المستطيل

قانون مساحة المستطيل وما هو قانون مساحة المربع قانون مساحة المستطيل بمعلومية طول قطره قانون قطر المربع تجدون كل تلك الموضوعات من خلال مقالنا هذا

قانون مساحة المستطيل

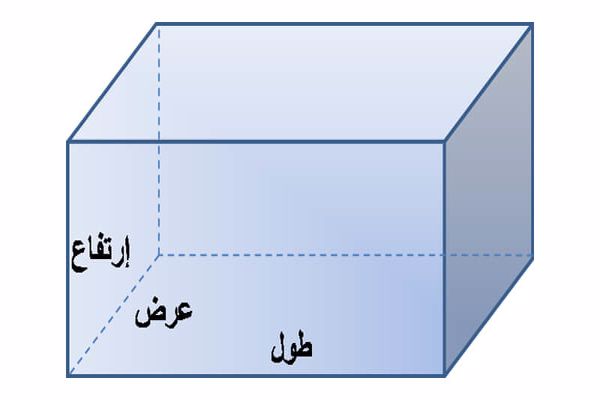
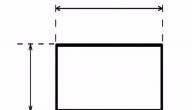
1-قانون محيط المستطيل ومساحته، يعتبر المستطيل من أهم الأشكال الهندسية في العلوم التطبيقية والتكنولوجيا؛ لأنه شكل مربع ثنائي الأبعاد له أربع زوايا قائمة عند 90 درجة مئوية وأربعة جوانب عمودية، بحيث يتساوى زوجان مع كل من الأمثلة الأكثر شيوعًا مشهور من خاص، المستطيل مربع مما يعني أن المربع مربع الشكل هذا يعني أنه مستطيل الأضلاع متطابقة تمامًا والمستطيل هو حالة خاصة من متوازي الأضلاع.
2-نظرًا لأن المستطيل هو شكل ثنائي الأبعاد يتميز بوجود بعدين، عرض وطول، فيمكن حساب محيطه من المعلومات المعروفة للجميع عن المضلعات الرباعية المنتظمة، وبالتالي محيطه هو مجموع الأطوال من جوانبها،
3-مساحة المستطيل = الطول × العرض.
4-محيط المستطيل = 2 (الطول + العرض).

قانون مساحة المربع

1-المساحة تمثل الجزء المحصور بين نطاق معين على سطح ما و من ابسط الاشكال لها هى تلك المناطق المحصورة بين اربعة اضلاع سواء ذات اطوال متساوية و كل ضلعين متقابلين متوازيين و كل ضلعين متتاليين متعامدين , مما يكون ما يعرف بالمربع و تتمثل وحدة قياس المساحة في الوحدة المربعة ففي الامتار تكون مترمربع و في السم تكون سم مربع الخ , في النظام الدولي الوحدة القياسية لحساب المساحة هى المتر المربع و التي تعبر عن مساحة مربع طول ضلعه متر , بالطبع لا تكتفي المساحات على الاشكال المربعة و انما هناك الاشكال المثلثة و المستطيلة و التي على شكل شبه منحرف و دائرة و غيرها من الاشكال و لكل شكل صيغة معينة لحساب المساحة الخاصة به .
2- المربع واحد من المضلعات الرباعية و هو عبارة عن مضلع رباعي منتظم مغلق اضلاعه متساوية في الطول و متعامدة و تشكل معًا اربع زوايا او اربع رؤوس و يمكن ان يتم تشكيل المربع من خلال جمع مثلثين قائمي الزاوية و متساويي الساقين من عند الوتر , يعتبر المربع ذو اهمية كبيرة في المفاهيم الهندسية حيث تم بناء تعريف المساحات لمختلف الاشكال الهندسية على الوحدات المربعة , يمثل حساب مساحته ابسط عمليات حساب المساحة و له اكثر من طريقة لحساب المساحة و لكن قبل التعرف على طرق حساب مساحة المربع يجب ان تتعرف على خصائص المربع
3-مساحة المربع = طول الضلع * نفسه

قانون مساحة المستطيل بمعلومية طول قطره

1-مساحة المستطيل = ( طول الضلع الأول (الطول) * طول الضلع الثاني (العرض)). محيط المستطيل = 2 * ( طول الضلع الأول (الطول) + طول الضلع الثاني(العرض)).
2- (القُطر) مرفوع للقوة 2 = (الطول مرفوع للقوة 2 * العرض مرفوع للقوة 2). أي أن القُطر يساوي جذر العملية الحسابية الناتجة من تربيع الطول مضروباً في تربيع العرض، وتُستخدم مساحة المستطيل لأيجاد مساحة قطعة أرض مثلاً وايجاد العمليات اللازمة للبناء، أو مساحة ملعب كُرة قدم أو مسبح او غيرها،وتُقاس المساحة بشكل عام بالوحدة القياسية المربعة، حسب كُبرها فمثلاً المساحات على الكتاب او الدفتر أو اللوح المدرسي تُقاس بالسانتيميتر المربع،أما مساحات البناء والملاعب وغيرها من الأمور المتوسطة فتُقاس بالمتر المربع. وفي المُدن والمساحات الكُبرى تُقاس بالكيلو متر المرُبع.

قانون قطر المربع

1-قطر المربع عبارة عن خط مستقيم يربط بين إحدى زوايا المربع، والزاوية المقابلة له، ويمكن استخدام نظرية فيثاغورس لإيجاد طول قطر المربع، حيث إن قطر المربع يقسم المربع إلى مثلثين لهما زاوية قائمة، وكل مثلث له ضلعان متساويان في الطول، ويساويان طول ضلع المربع، وبالتالي تستخدم نظرية فيثاغورس لإيجاد طول الوتر الذي يمثل القطر، وذلك على النحو الآتي
2- أ2 + ب2 = جـ2. حيث أ، ب هما أضلاع المثلث، و جـ هو الوتر، أو القطر.
3-ويمكن أيضاً إيجاد طول قطر المربع من خلال العلاقة الآتية: طول قطر المربع = طول ضلع المربع × الجذر التربيعي للرقم 2.