محيط المستطيل والمربع

محيط المستطيل والمربع ومساحة المربع وإيجاد طول وعرض المستطيل وخصائص المستطيل والمربع، هذا ماسوف نتعرف عليه فيما يلي.

محيط المستطيل والمربع

1-المستطيل:
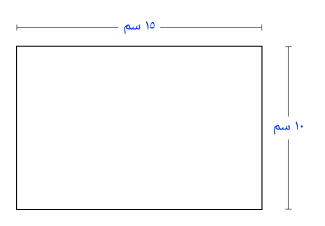
المستطيل هو شكل ثنائي الأبعاد وشكل رباعي الزوايا الأربع القائمة، ويترتب على ذلك أن للمستطيل زوجان من الأضلاع المتقابلة والمتساوية.
المساحة = الطول × العرض.
المحيط = (الطول + العرض) × 2.
2-المربع:
المربع هو مضلع منتظم يتكون من أربعة جوانب متعامدة تشكل أربع زوايا قائمة
المساحة = طول الضلع x نفسه.
المحيط = طول الضلع × 4.

مساحة المربع

مساحة المربع يتم تصنيف المربع على أنه شكل رباعي متساوي الأضلاع، ويتم التعبير عن الحيز الذي يشغل المنطقة المحصورة بين أضلاع المربع بمصطلح مساحة المربع (بالإنجليزيّة: Area of square)،ولإيجاد مساحة المربع لا بد من معرفة طول ضلعه كما يمكن معرفة مساحة المربع من خلال معرفة طول قطره أيضًا؛ وطول القطر هو الخط المستقيم الممتد من أحد زوايا المربع إلى الزاوية المقابلة لها، ويمكن حساب مساحة المربع كما يأتي
-مساحة المربع باستخدام طول الضلع يمكن حساب مساحة المربع باستخدام طول الضلع من خلال التعويض في المعادلة الآتية: مساحة المربع= طول الضلع * طول الضلع، وبالرموز A= S * S = S^2، وتمثل الرموز ما يأتي:
– A: مساحة المربع
– S: طول الضلع.
-ويجدر الانتباه إلى أن وحدة قياس المساحة هي مربع الوحدة؛ ففي حال حساب مساحة مربع طول ضلعه مُقاسًا بوحدة سم (سنتيمتر) فإن مساحة المربع هنا تكون بوحدة سم2 (سنتيمتر مربع)، بينما في حال حساب طول الضلع بوحدة م (متر) فإن مساحة المربع تكون بوحدة م2 (متر مربع) وهكذا.

إيجاد طول وعرض المستطيل

-باستخدام مساحة المستطيل
يُمكن إيجاد مساحة المستطيل من خلال معرفة طوله وعرضه، وتجدر الإشارة إلى أن الطول والعرض عبارة عن قيمتين مستقلتين، وبالتالي فإنه لا يمكن إيجاد الطول، والعرض من خلال معرفة المساحة فقط، أما في حال معرفة قيمة أحدهما فإنه يمكن إيجاد الأُخرى، ومساحة المستطيل تساوي الطول × العرض، وبالتالي فإنه:
في حال معرفة عرض المستطيل، يمكن إيجاد الطول من خلال العلاقة طول المستطيل = المساحة / العرض.
وفي حال معرفة طول المستطيل، يمكن إيجاد عرضه من خلال العلاقة عرض المستطيل = المساحة / الطول.
-باستخدام محيط المستطيل
يُمكن إيجاد طول، أو عرض المستطيل من خلال معرفة محيطه، حيث أن محيط المستطيل يساوي المسافة التي تُحيط بالشكل الخارجي، ويساوي مجموع أطوال أضلاعه، ويُعبَر عنه بالعلاقة الآتية:
محيط المستطيل = الطول + الطول + العرض + العرض
محيط المستطيل = 2 × الطول + 2× العرض
محيط المستطيل = 2 × (الطول + العرض).

خصائص المستطيل والمربع ومتوازي الاضلاع

1-خصائص المربع
-جميع أضلاع المربع متساوية.
-جميع أضلاع المربع المتقابلة المتساوية متوازية.
-المربع حالة خاصة من حالات متوازي الأضلاع.
-جميع زوايا المربع متساوية.
-جميع زوايا المربع المتقابلة متساوية.
-مجموع كل من الزاويتين المتتاليتين يساوي مائة وثمانون درجة.
-جميع زوايا المربع الأربعة قائمة.
-كل قطرين في المربع ينصف أحدهما الآخر.
-دوماً ما ينصف قطري المربع الزوايا.
-القطران متعامدان، كما أنها دائماً ما يكونوا متطابقان.
-قانون حساب محيط المربع هو (طول الضلع)× 4.
-قانون حساب مساحة المربع هو مربع طول الضلع.
2-خصائص المستطيل
-ليست جميع أضلاع المستطيل متساوية.
-جميع أضلاع المستطيل المتقابلة المتساوية متوازية.
-المستطيل حالة خاصة من حالات متوازي الأضلاع.
-جميع زوايا المستطيل متساوية.
-جميع زوايا المستطيل المتقابلة متساوية.
-مجموع كل من الزاويتين المتتاليتين يساوي مائة وثمانون درجة.
-جميع زوايا المستطيل الأربعة قائمة.
-كل قطرين في المستطيل ينصف أحدهما الآخر.
-ليس دوماً ما ينصف قطري المستطيل الزوايا.
-لا يتعامد دوماً قطري المستطيل، كما أنهما لا يكونوا متطابقان.
-قانون حساب محيط المستطيل هو 2×(الطول + العرض).
-قانون حساب مساحة المستطيل هو الطول× العرض.
3-خصائص متوازي الأضلاع
-كل زاويتين في متوازي الأضلاع متقابلتين متساويتين.
-كل زاويتين تقعان على ضلع واحد أي أنهما متحالفتين ومتكاملتين بحيث يبلغ مجموعهما مائة وثمانون درجة.
-في الحالة التي يكون بمتوازي الأضلاع زاوية قائمة، فإن جميع زواياه الأخرى سوف تكون قائمة أيضاً، وعلى ذلك فإنه يكون حينها مستطيل كما قد يكون مربع وهو ما يعد بعض الحالات الخاصة من متوازي الأضلاع.
-من الخصائص المميزة لمتوازي الأضلاع أنه يشتمل على قطرين، ويقصد بالقطرين ما يمكن رسمه من خطوط مستقيمة بين أحد زوايا رؤوس متوازي الأضلاع أي رؤوسه بحيث يصل إلى الرأس المقابل له، ولقطري متوازي الأضلاع خصائص تميزها وهي:
-ينصف كل قطر منهما القطر الآخر.
-كل قطر في متوازي الأضلاع يقسمه إلى مثلثين متطابقين.