مساحة المستطيل مختلف الأضلاع

مساحة المستطيل مختلف الأضلاع نتعرف عليها من خلال مقالنا هذا كما نذكر لكم حساب محيط المستطيل ومفهوم المساحة وخصائص المستطيل وما هو متوازي المستطيلات وخصائصه.

مساحة المستطيل مختلف الأضلاع

يمكن حساب مساحة المستطيل مختلف الاطلاع بطريقتين وهم:
الطريقة الاولى :
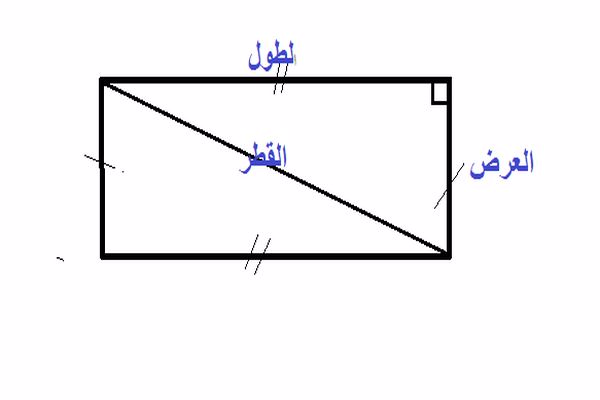
تطبيق نظرية فيثاغورث عندما يكون معلوم لديك طول احد اجناب المستطيل و قطره هنا تستطيع تطبيق نظرية فيثاغورث للحصول على الحد الثاني , من المعروف انه من خواص المستطيل ان كل زواياه الاربع قوائم اي ان كل زاوية يحدها ضلعين من اضلاع المستطيل احدهما يكون الطول و الآخر العرض هما ضلعي الزاوية القائمة او ما نطلق عليه ضلعي القائمة و القطر هنا يمثل الوتر او الضلع المقابل للزاوية القائمة , لذا فانه يمكن تطبيق نظرية فيثاغورث الخاصة بالمثلث القائم الزاوية و تساعدنا في الحصول على ايًا من ضلعي القائمة او حرفي المستطيل بمعلومية الضلع الثاني و الوتر .
معادلة نظرية فيثاغورث
مربع طول الوتر = مجموع مربعي ضلعي القائمة .
في حال المستطيل
مربع القطر = مرع الطول + مربع العرض .
القوانين الفرعية
الطول = الجذر التربيعي لمربع القطر – مربع العرض .
العرض = الجذر التربيعي لمربع القطر – مربع الطول .
مثال: مستطيل طول قره 10 سم و عرضه يساوي 6 سم احسب مساحة المستطيل .
الحل:
طول المستطيل = الجذر التربيعي لمربع القطر – مربع العرض
= الجذر التربيعي لـ 100 – 36
= الجذر التربيعي لـ 64 = 8 سم .
مساحة المستطيل = الطول X العرض = 6 X 8 = 48سم2
الطريقة الثانية:
لحساب مساحة المستطيل هناك معادلة اساسية من خلالها يتم حساب مساحتة و هى:
مساحة المستطيل = الطول ( ل ) X العرض ( ع ) و الناتج يحسب بالسم المربع او المتربع او ايًا كانت ودة القياس المستخدمة المهم ان وحدة قياس المساحة هى التربيع .
مثال: مستطيل طوله يساوي 10 سم و عرضه يساوي 7 سم اوجد مساحة المستطيل.
الحل:
مساحة المستطيل = ل X ع = 10 X 7 = 70 سم2
و من خلال هذا القانون تستطيع الحصول على الطول او العرض بقوانين متفرعة منه و لكن هنا يجب ان يكون بالمعادلة مجهول واحد اي انه للحصول على طول المستطيل يكون معطى لنا العرض و المساحة او العكس .
الطول ( ل ) = المساحة \العرض ( ع )
العرض ( ع ) = المساحة \ الطول ( ل )
مثال : – مستطيل مساحته 72سم2 و طوله يساوي 12 سم او جد عرضة .
الحل:
ع = المساحة \ الطول = 72\12 = 6 سم
مثال : – مستطيل مساحته 36 سم2 و عرضه يساوي 4 سم احسب طوله .
الحل:
ل = 36\4 = 9 سم

حساب محيط المستطيل

يتم حساب محيط المستطيل عن طريق القوانين الآتية:
القانون الأول
يتم قياسه محيطه إذا تم معرفة طوله وعرضه، كما في القانون الآتي:
محيط المستطيل= 2 × طول الضلع الأول (الطول) + طول الضلع الثاني (العرض).
القانون الثاني
يمكنك إيجاد محيط المستطيل في حالة معرفة مساحته وطول أحد أضلاعه وذلك من خلال القانون الآتي:
محيط المستطيل= (2 × المساحة + 2 × مربع الطول) / الطول
محيط المستطيل= (2 × المساحة + 2 × مربع الطول) / العرض
القانون الثالث
يمكنك إيجاد محيط المستطيل في حالة معرفة قطره وطول أحد أبعاده وذلك من خلال القانون الآتي:
محيط المستطيل= 2 × (الطول + (مربع القطر – مربع الطول) ^ (2/1))
محيط المستطيل= 2 × (العرض + (مربع القطر – مربع العرض) ^ (2/1)

مفهوم المساحة

حيث إنّ المساحة هي مصطلح رياضي يمكن تعريفه بأنّه الحيز الذي يشغله جسم ثنائي الأبعاد في الفضاء، ويمكن استخدام المساحة في العديد من التطبيقات العملية مثل البناء والهندسة المعمارية والعلوم والزراعة وحتى مقدار السجادة التي سيتم وضعها على أرضية الغرف في المنزل، ويمكن تحديد المساحة بكل سهولة بالنسبة إلى الأشكال الهندسية المعروفة مثل المربع أو المستطيل، حيث يمكن ذلك من خلال معرفة الطول والعرض ثم تطبيق المعادلات الرياضية الخاصة بكل شكل هندسي، ولكن إذا كان الشكل الهندسي أكثر تعقيدًا مثل المثلث أو الدائرة فإنه هناك حاجة ضرورية لاستخدام صيغ رياضية أكثر تعقيدًا، وقد كان أول من قام بدراسة المساحة وتأليف كتب في الرياضيات هم الأشخاص الذين كانوا في منطقة بلاد ما بين النهرين، كما عرف مهندسو الأهرامات في مصر أهمية إيجاد صيغ رياضية لإيجاد مساحة مثلث ثنائي الأبعاد لبناء الأهرامات، كما استخدم إسحاق نيوتن مفهوم المساحة لتطوير المفاهيم المتعلقة بحساب التفاضل والتكامل أيضًا.

خصائص المستطيل

من خلال التعريف بالشكل الهندسي ثلاثي الأبعاد المستطيل يمكن التوصل إلى خصائصه والتي تحدد كيف يتم تكوين المستطيل، فالأشكال الهندسية عديدة وكثيرة وما يمزها عن بعضها البعض هو خصائص كل شكل هندسي والتي تختلف من شكل إلى آخر، وخصائص المستطيل هي:
1-كل ضلعين متقابلين في المستطيل متساويان في الطول.
2-المستطيل هو أحد أشكال متوازي الأضلاع، إلا أن زواياه قائمة.
3-قطرا المستطيل متساويان في الطول.
4-قطرا المستطيل ينصف كل منهما الآخر.
5-كل ضلعين متقابلين في المستطيل متوازيين.
6-مجموع زوايا المستطيل 360 درجة وهم أربع زوايا كل زاوية تساوي 90 درجة.

ما هو متوازي المستطيلات؟

متوازي المستطيلات: هو عبارة عن شكل هندسي ثلاثي الأبعاد على هيئة مجسم ثلاثي الأبعاد (طول وعرض وارتفاع، وهو شكل يشبه الصندوق على شكل مستطيل، ويتميز متوازي المستطيلات بمجموعة من الخصائص تميزه عن غيره من المجسمات الأخرى.
خصائص متوازي المستطيلات:
1-له ستة أوجه كل منها على شكل مستطيل.
2-نستطيع إيجاد مساحة متوازي المستطيلات من خلال ايجاد المساحة الجانبية = محيط القاعدة × الارتفاع، المساحة الكلية= المساحة الجانبية +مساحة القاعدتين.
3-يحتوي على أربعة جوانب مستطيلة الشكل وقاعدتين متوازيتين ومتطابقتين.
4-له ثمانية زوايا وجميعها قوائم.
5-يسمى متوازي المستطيلات بذلك الاسم، لأنه يتكون من ستة أوجه مستطيلة كل شكل يوازي الشكل الذي يقابله.
6-متوازي المستطيلات هو مجسم ثلاثي الأبعاد (الطول والعرض والارتفاع).
7-يتشابه مع المثلث ولكن الاختلاف يكون في أطوال الأضلاع.