أنواع المصفوفات في الحاسوب والأداء والقيود للمصفوفة في الحاسوب ونبذة عامة عن المصفوفات وخواص المصفوفات و العمليات التي تجري عليها كل هذا تجدونه في ذلك المقال.
محتويات المقال
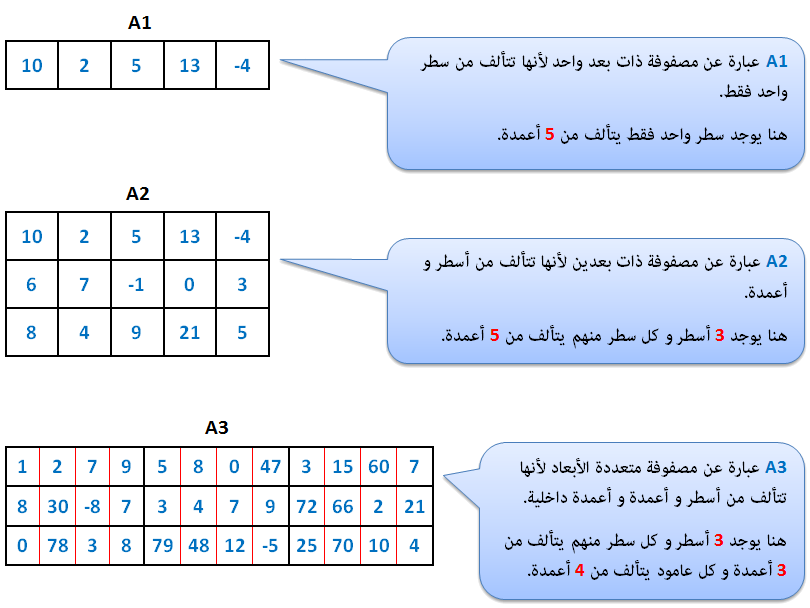
أنواع المصفوفات في الحاسوب
المصفوفة هي تركيبة من البيانات يتم إنشائها بشكل برمجي في الحاسوب، يمكنها تخزين العديد من العناصر من نفس النوع و كل عنصر يحمل قيمة، يتم حجز مساحة من الذاكرة لتحمل قيمة و مكان كل عنصر بشكل متسلسل، المصفوفة لها سعة ثابتة و لا تتغير خلال وقت التنفيذ لهذا يجب تحديد سعة المصفوفة خلال وقت البرمجة وتنقسم لثلاثة أنواع على النحو التالي:
1-يمكن للمصفوفة أن تكون أحادية أو ذات بعد واحد (One dimensional array) و هذا النوع يسمى Vector في مادة الرياضيات.
3-يمكن للمصفوفة أن تكون ثنائية أو ذات بعدين (Two dimensional array) و هذا النوع يسمى Matrix في مادة الرياضيات.
3-يمكن للمصفوفة أن تكون متعددة الأبعاد (Multidimensional array).
الأداء والقيود للمصفوفة في الحاسوب
يتم تمثيل العناصر في الذاكرة في شكل مناطق متجاورة ، هذا ما يجعل عمليات الإدراج والحذف مستحيلة، إلا إذا قمت بإنشاء مصفوفة جديد فمن الضروري نسخ جميع العناصر من الجدول الأصلي إلى الجدول الجديد، ومن ثم تحرير مساحة الذاكرة المخصصة للمجموعة القديمة، أو يمكن استخدام المصفوفة الديناميكية. في بعض لغات البرمجة اسم المصفوفة هو مؤشر لأول عنصر في الفهرس وتوجد حالات قد تشكل مشكلة في النظام أو ثغرة أمنية أو خطأ في سير البرنامج و هي الإشارة إلى عنصر خارج المجموعة على سبيل المثال واذا تم تصميم مصفوفة تحتوي على 50 عدد صحيح وقمت بكتابة قيمة إلى المؤشر أكبر من 50 ، فهذه القيمة ستكتب خارج ذاكرة المخصصة للمصفوفة، ولكن في بعض الأحيان نظام التشغيل يمنع هذا وسعة المصفوفة المحدود له ميزة ثبات زمن الوصول إلى قيمة العنصر، بغض النظر عن مكان العنصر المطلوب. ويرجع ذلك إلى أن العناصر هي مجموعة متجاورة في الذاكرة .
نبذة عن المصفوفات
تعرف المصفوفة في الرياضيات بأنها مجموعة مستطيلة من الأرقام منتظمة بشكل أعمدة وأسطر ويدعى كل جزء رقم في المصفوفة بعنصر أو مدخل. كمثال على المدخلات في المصفوفة أعلاه 1, 9, 13, 20, 55 ,4. يدل عادة على أي مدخل في مصفوفة ما باسم المصفوفة بحرف لاتيني صغير وأسفله رقمين صغيرين بحيث يمثل الرقم الأول رقم الصف والثاني رقم العمود مثل الشكل المرفق ويمكن جمع وطرح المصفوفات ذات نفس القياس. كما يمكن ضرب المصفوفات بأنسجام معين في القياس ولهذه العمليات العديد من خصائص الحساب العادي, باستثناء أن ضرب المصفوفات ليس بعملية تبديلية, وبشكل عام يمكن أن نقول أن A.B لا يساوي B.A. تعرف المصفوف المؤلفة من صف واحد أو عمود واحد بمتجه. أما المصفوفة ذات القياس الأكبر تعرف بموتر.
تعتبر المصفوفات من إحدى أهم مفاتيح الجبر الخطي. فيمكن أن تستخدم المصفوفات في حل النقل الخطي. يتوافق ضرب المصفوفات مع النقل الخطي الدالة المركبة.
– كما يمكن للمصفوفات تتبع المعاملات في نظام المعادلات الخطية ويمكن تعريف المصفوفة عامة على أنها دالة رياضية خطية تحول مجموعة بداية أي انطلاق (مجال) إلى مجموعة وصول أو نهاية (مدى). مجموعة الانطلاق والوصول يمكن أن تكون متكونة من أعداد صحيحة أو عقدية أو أشعة من الأعداد كما يمكن أن تكون هاتان المجموعتان متكونة بدورها من دالات رياضية أو أشعة دالات رياضية. ويمكن أن نرمز للمصفوفة بمعقفين يكتب بينهما عناصر المصفوفة كما هو مبين أسفله
خواص المصفوفات و العمليات التي تجري عليها
تتساوى المصفوفتان A,B وتكتب (A=B) اذا كان :
1- كل من A,B من القياس نفسه .
2- كل عنصر في A يساوي نظيره في الموقع B .
2-ضرب المصفوفات بأعداد:-
اذا كانت A مصفوفة وكان K عددا حقيقيا فأن حاصل ضرب A في K يكتب KA او AK هو المصفوفة الناتجة من ضرب جميع عناصر A في K ويمكن أن نعرفها كما يأتي:-
اذا كان A=(aij)فأن KA=AK=(Kaij)
3 – جمع وطرح المصفوفات :-
يمكن جمع المصفوفتين A=(aij) , B=(bij) اذا كانتا من نفس السعة ويكون ناتج الجمع مصفوفة ويرمز لها بالرمز A+B ونحصل عليها بجمع العناصر المتناظرة في المصفوفتين أي ان:-
A+B=(aij + bij)
-ولاتعرف عملية الجمع لمصفوفتين اذا كانتا من سعتين مختلفين ويمكن تعريف عملية طرح المصفوفات بأعتبارها عملية عكسية لعملية الجمع وذلك بأن تقول :أذا كانت A , B مصفوفتين من القياس نفسه فأن A-B هي مصفوفة نحصل عليه بطرح B من العناصر المناظرة في
التطور التاريخي للمصفوفات
1-يمثل أول شكل لاستخدام المصفوفات عند حل المعادلات باللغة الصينية ويطلق عليه “تسعة فصول من الفن الرياضي”. ويتضمن أيضًا المبدأ المحدد والذي يمكن إرجاعه إلى ما بين 300 قبل الميلاد و200 بعد الميلاد. وفي عام 1683 نشر عالم الرياضيات الياباني سيكي تاكاكازو ورقة عن المصفوفات.
2-يليه العالم الألماني جوتفريد لايبنيز نشر ورقة بحثية عن المصفوفات عام 1693 ونشر غابرييل كرامر بعد ذلك قواعده الحسابية في عام 1750 وركزت نظرية المصفوفة المبكرة على دور المحدد بدلاً من أن تكون مستقلة عن المصفوفة ولم يظهر مفهوم المصفوفة بشكل مستقل مع آرثر كايلي ونظرية المصفوفة الخاصة به حتى عام 1858.
3-نظرية المصفوفة هي فرع من فروع الرياضيات تركز على دراسة المصفوفات وفي الواقع. وتعتبر أحد فروع الجبر الخطي لذلك فهو يغطي بالفعل موضوعات متعلقة بنظرية الرسم البياني والجبر والتوافقيات والإحصاءات وتمثل المصفوفة مجموعة مستطيلة من الأرقام وفي عام 1848 كما صاغ عالم الرياضيات الإنجليزي جيمس جوزيف سيلفستر مصطلح المصفوفة كاسم لمجموعة من الأرقام المرتبة.
4-وفي عام 1855 اقترح آرثر كايلي مصفوفة لتمثيل العناصر الخطية وتعتبر هذه الفترة بداية نظرية الجبر الخطي والمصفوفة. وتعتبر دراسة الفراغات المتجهة في مجالات محددة فرعًا من الجبر الخطي المفيد في نظرية التشفير والذي يؤدي بشكل طبيعي إلى البحث واستخدام المصفوفات في مجالات محددة في نظرية التشفير و الوحدة عبارة عن تعميم لفضاء المتجه فيتم التفكير في الأمر على أنه مساحة للناقلات على الحلبة.
5- وأدى هذا إلى البحث حول حلقات المصفوفات ولا تعتبر نظرية المصفوفة في هذا المجال فرعًا من فروع الجبر الخطي. إلا إذا كانت الحلقة الموضحة متبادلة. والنظرية والنتائج في نظرية كيلي هاملتون مقبولة إذا كانت الحلقة المحددة حقلًا مثاليًا رئيسيًا. فإن شكل سميث الطبيعي يكون متوافقًا ولكن البقية قابلة للتطبيق فقط في حالة مصفوفة ذات معقد أو حقيقية الأعداد.