بحث عن المتجهات، ومقدمة بحث عن المتجهات، وتعريف المتجهات، وخصائص المتجهات، ومميزات المتجهات، وتاريخ المتجهات، وخاتمة بحث عن المتجهات، نتناول الحديث عنهم بشيء من التفصيل خلال المقال التالي.
محتويات المقال
بحث عن المتجهات
العناصر
1. مقدمة بحث عن المتجهات.
2. تعريف المتجهات.
3. خصائص المتجهات.
4. مميزات المتجهات.
5. تاريخ المتجهات.
6. خاتمة بحث عن المتجهات.
مقدمة بحث عن المتجهات
– تحليل متجه بشكل مستقل للتعبير عن قوانين الكهرومغناطيسية الجديدة، التي اكتشفها الفيزيائي الإسكتلندي جيمس كليرك ماكسويل منذ ذلك الوقت، أصبحت المتجهات أساسية في الفيزياء والميكانيكا والهندسة الكهربائية، وغيرها من العلوم لوصف القوى حسابيًا.
– المتوازي المتجه للجمع والطرح طريقة واحدة لإضافة، وناقل المتجهات هي وضع ذيولها معًا ثم تزويد جانبين آخرين لتشكيل متوازي الأضلاع، المتجه من ذيولهم إلى الزاوية المقابلة من متوازي الأضلاع، يساوي مجموع المتجهات الأصلية المتجه بين رؤوسهم يبدأ من الموجه الذي يتم طرحه يساوي فرقهم.
تعريف المتجهات
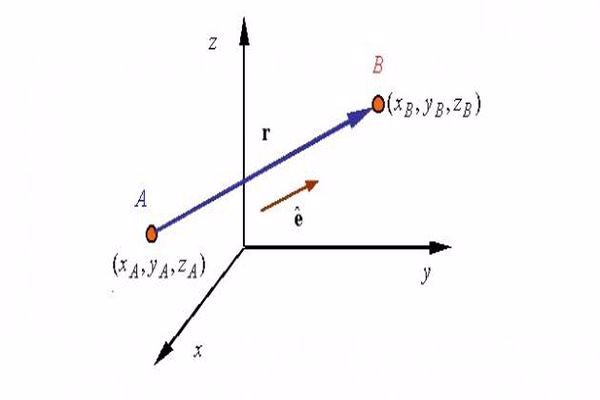
– المتجهات هي الشيء المطلوب لعملية نقل النقطة ” أ ” إلى النقطة ” ب ”، و تم استخدام مصطلح المتجهات لأول مرة من خلال علماء الفلك في القرن الثامن عشر و الذين كانوا يبحثون في دراسة الكواكب و الشمس، إن حجم المتجهات يشير إلى المسافة بين نقطتين و يشير كذلك إلى اتجاه النقل من النقطة ” أ ” إلى النقطة ” ب ”.
– جميع العمليات الجبرية الرياضية التي يتم عملها على الأعداد الحقيقية مثل الطرح والجمع و الضرب يكون لها نظائر قريبة من المتجهات أو النواقل، والمفهوم الأكثر شمولية للمتجهات أو النواقل هو أنها عدد من عناصر المساحة الناقلة، وتفيدنا المتجهات كثيرا في الكثير من الدراسات العلمية حيث أنه لا يكفي قياس قوة معينة بل يجب معرفة مقدار هذه القوة و اتجاهها كذلك.
خصائص المتجهات
1. تساوي المتجهات
حيث أن المتجهات يكونان متساويان في حال امتلكا نفس الطول أي نفس المقدار، ويشيران لنفس الاتجاه أي أنهما لهما نفس الاتجاه، فمثلاً يمكننا القول أن متجهين يشيران للشمال ويبلغ مقدار كل متجه منهما 5 إذ نفهم أن هذان المتجهان متساويان.
2. جمع المتجهات
من الممكن جمع المتجهات وذلك من خلال جمع المركبات التي تكون متجهة معاً، بمعنى أنه يتم جمع المركبات السينية معاً وجمع المركبات الصادية ثم القيام بجمع المركبات العينية، كل مركبة منهم يتم جمعها على حدها، ومن الممكن القيام بجمع المتجهات بواسطة طريقة هندسية والتي يتم فيها وضع المتجه الأول ثم يتم وضع ذيل المتجه الثاني وهكذا، وبالنهاية يتم رسم سهم بدءاً من ذيل المتجه الأول حتى رأس المتجه الأخير، ويكون حاصل الجمع هو المتجه الأخير الذي رُسم وهو ما يعرف باسم المتجه المحصل، ويخضع جمع المتجهات لكل من الخاصيتين التبديلية والترابطية للجمع.
3. ضرب المتجهات مع بعضها البعض
حيث يوجد نوعان من الضرب أثناء ضرب المتجهات، فحين القيام بضرب متجهين ضرب نقطي فإنه عند ذلك ستنتج كمية قياسية وهذا النوع من الضرب يعرف بالضرب القياسي، ولكن في حال ضرب متجهين ضرب تقاطعي فإنه سوف يكون الناتج عبارة عن متجه جديد يقع عمودي على كلا المتجهين اللذين تم القيام بضربهما، وهذا النوع من الضرب يعرف باسم الضرب الاتجاهي.
4. المتجه السالب
في حال لو كان لدينا المتجه A فنفهم أن المتجه السالب منه يكون هو المتجه الذي يعطي نتيجة صفر حين القيام بجمعه مع المتجه A، والمتجه السالب له نفس النسخة الموجبة إلا أنه يكون في عكس اتجاهه، أي أن الدرجة التي بينهما تكون 180.
5. طرح المتجهات
تعتبر عملية طرح المتجهات نفس عملية الجمع، ولكن بدلا من القيام بجمع متجهين فإنه يتم القيام بإضافة المتجه الأول إلى سالب المتجه الثاني، بمعنى أنه يتم إضافة المتجه الثاني بعد القيام بعكس اتجاهه.
مميزات المتجهات
1. تتميز بتوفير إمكانية الجهات الخاصة بالعقار.
2. تعمل على التمييز بين الكميات المتجهة والكميات السلمية التي يطلق عليها الكميات العددية والكميات القياسية.
3. تجرى هذه العملية التي لها علاقة بالمتجهات للعمليات الحسابية الأساسية.
4. يساعد هذا التطبيق بالعمل على إدراك الفرق بين الكميات السليمة والكميات المتجهة.
5. تقوم الكمية المتجهة بتصنيف الكميات الفيزيائية إلى كميات عددية وكميات متجهة، وقد يتم التمثيل إلى هذه المتجهات من خلال الرسم، ويتم تحليل هذه المتجهات في العديد من المستويات التي تحتوي على محورين متعامدين، لإيجاد قيمة خاصة بالمتجهات التي يتم التعرف عليها من خلال المركبات السينية والصادية الخاصة به.
تاريخ المتجهات
تطور مفهوم المتجه عما نعرفه اليوم تدريجيًا على مدى أكثر من 200 عام، وقدم حوالي عشرة أشخاص مساهمات كبيرة فيه، ولقد قام Giusto Bellavitis بتجريد الفكرة الأساسية في عام 1835 عندما أسس مفهوم “equipollence” وتم تقديم مصطلح المتجه من قبل ويليام روان هاميلتون كجزء من quaternion وهو مجموع q = s + v من عدد حقيقي s يسمى أيضًا scalar وناقل ثلاثي الأبعاد، واعتبر هاملتون أن المتجه v هو الجزء التخيلي من quaternion:، والعديد من علماء الرياضيات الآخرين طوروا أنظمة شبيهة بالنواقل في منتصف القرن التاسع عشر، بما في ذلك أوغستين كوشي، هيرمان جراسمان، أغسطس موبيوس، كونت دي سان-فينانت، وماثيو أوبراين.
خاتمة بحث عن المتجهات
المّتجهة هي أحد الطرق ووسائل المستخدمة في التحليل الاتجاهي، حيث تمثل بسهم ينطلق من نقطٍة معينٍة وينتهي إلى أخرى وفي اتجاٍه معين، فتمثل نقطة بدأ هذا السهم أو المتجه نقطة التأثير، أّما مقدار المتجه فهو عبارٌة عن طول هذا المتجه، فيمثل الطول مقدار الكمية فقط، وأّما اتجاه المتجه فيمثل الاتجاه للكمية الُمقاسة في الفضاء لنا.