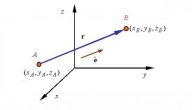
بحث عن المتجهات في الفراغ

بحث عن المتجهات في الفراغ نقدمه لكم من خلال مقالنا هذا ويتكون من مقدمة بحث عن المتجهات في الفراغ وتعريف المتجه وعمليات على المتجهات وخصائص المتجهات وخاتمة بحث عن المتجهات.

بحث عن المتجهات في الفراغ

عناصر البحث
1-مقدمة بحث عن المتجهات في الفراغ
2-تعريف المتجه
3- عمليات على المتجهات
4- خصائص المتجهات
5- خاتمة بحث عن المتجهات

مقدمة بحث عن المتجهات في الفراغ

هناك بعض الأشياء في الفيزياء التي تحتاج إلى تحديد الكمية بدون الاتجاه، وبعض الأشياء تحتاج إلى تحديد الاتجاه والكمية معاً، ونقص أي شيء منهم قد يكون غير دقيق ويقع تحت الاختبار مرة أخرى فتحديد الكمية في الفيزياء يتشابه مع تحديد أو ذكر أسم الشخص س على سبيل المثال وقد يكون هذا التعريف غير دقيق، لأنه يحتاج إلى تعريف أكثر دقة مثل ذكر من هو وماذا يعمل أو أي توضيح لهذا الشخص س نظراً لتشابه الاسم مع ملايين آخرين، ممن يخضعون لنفس الاختبار هنا. لابد من توضيح المتجهات كالكمية والاتجاه معاً، وعلى نحو آخر إذا كان السؤال عن عدد الأشخاص المتواجدين داخل المكان ب، هنا تحتاج إلى ذكر العدد فقط أي المقدار فقط مثل هناك خمس عشر فرد داخل المكان ب، وهنا التعريف مكتمل لا يحتاج لتحديد الاتجاه.

تعريف المتجه

-المتجه عبارة عن كمية لها مقدار (حجم رقمي) واتجاه، هذا هو عكس العددية، وهي كمية لها فقط حجم وبدون اتجاه. لذلك، على سبيل المثال، قد تسير السيارة بسرعة 60 ميلًا في الساعة، هذه هي سرعة السيارة، وهي كمية عددية، لكن قد تكون سرعة السيارة 60 ميلًا في الساعة شمالًا، ولكي تكون سرعة، يجب أن يكون لها اتجاه.
-المسافة عبارة عن كمية عددية تخبرك إلى أي مدى تجولت في المنزل، مثلا 400 متر، نظرًا لأنه رقم قياسي، فإن الاتجاه الذي تقوم بتشغيله غير ذي صلة، الشيء الوحيد المهم هو إلى أي مدى سافرت.
– لكن الإزاحة هي كمية متجهة تقيس الفرق في وضعك من حيث بدأت إلى حيث انتهيت، وإذا انتهيت في نفس المكان الذي بدأت فيه، فإن الإزاحة تكون صفرية، يؤثر الاتجاه أو الاتجاهات التي تركتها على النزوح نظرًا لأن النزوح عبارة عن ناقل. يتم تمثيل المتجهات بشكل تخطيطي باستخدام سهم، يمثل السهم الطويل رقمًا كبيرًا ويمثل السهم الصغير رقمًا صغيرًا.

عمليات على المتجهات في الفراغ

1-طرح المتجهات
طرح المتجهات هي نفسها عمليّة جمع المتجهات مع فرق بسيط، فبدل جمع متّجهين نقوم بإضافة المتجه الأول إلى سالب المتجه الثاني. وهنا يجب أن تتعلم ما هو سالب المتجه؛ حيث أن سالب المتجه يكون من خلال عكس اتجاهه مع بقاء قيمته نفسها.
2-ضرب المتجهات
هناك نوعان لضرب المتّجهات؛ وهذان النوعان هما الضرب القياسي ونسميه الضرب النقطي، والضرب المتجهي ونسميه أيضًا الضرب التقاطعي، حيث أننا عندما نضرب متجهين ضربًا نقطيًا، فإن الناتج سوف يكون كميّة قياسيّة، أي لها مقدار وليس لها اتجاه، ولهذا يُعرَف هذا النوع من الضرب بالضرب القياسيّ، أما عندما نقوم بضرب متجهين ضربًا تقاطعيًا، سيكون الناتج متجهًا عموديًا على كل من المتّجهين الضروبين؛ ولهذا السبب يُعرَف بالضرب الاتّجاهي.
3-جمع المتجهات
يمكنك أن تجري عملية جمع المتجهات من خلال الطريقة البيانية والطريقة الحسابية وسأبين لك كل منهما فيما يأتي:
1-الطريقة البيانية:
لو فرضنا أن لديك متجهان الأول هو a، والثاني هو المتجه b ، يمكنك أن تجري عملية الجمع بينهما ( a + b)، من خلال رسم المتجه a بمقداره واتجاهه الصحيح، ومن ثم تضع ذيل المتجه b على رأس المتجه a ونرسمه، ومن ثم نرسم خطًا بدايته في في ذيل a ونهايته في رأس b، ويكون ذدا الخط الناتج هو مجموع المتجهين.
2-الطريقة التحليلية:
بعد تحليل المتجهين المراد جمعهما إلى مركباتها السينية والصادية والزينية، نقوم بجمعهما من خلال جمع المركبات المتشابهة كما يأتي:
a = ax +ay +az
b = bx + by +bz
a+b= (ax+bx)+(ay +by) +(az +bz)

خصائص المتجهات

1-المتجهات السالبة مجموعها صفر
إن المتجه السالب مجموعه ببساطة يساوي صفراً وذلك عندما يتم جمع هذا المتجه مع متجه آخر له نفس المقدار لكنه متجه موجب حتى لو كان في الاتجاه المعاكس له أي أن مقدار الزاوية 180 درجة.
2-عملية طرح المتجهات تساوي عملية الجمع
مثلما قلنا في السابق فإن عملية الطرح تساوي عملية الجمع بين المتجهات حيث تتم إضافة كل من المتجه الأول لسالب المتجه الثاني على أن تكون تلك الإضافة الثانية بعكس اتجاه المتجه السابق.
3-عملية الضرب تتم بكمية قياسية
من أجل أن تتم عملية الضرب بنجاح بين المتجهات لابد أن تتم بكمية قياسية وذلك لأن عملية الضرب هذه لا تتم إلا بمقدار التغيير في طول أي متجه أو التغيير في مقداره بينما الاتجاه لن يتغير إلا بعد الضرب في أي رقم.
4-يمكن الجمع بين المتجهين معاً
يمكن الجمع بين متجهّين أو أكثر معاً وذلك من خلال وسيلة هندسية معينة ومحددة فعلى سبيل المثال يمكن وضع المتجه الأول في تتابعية مع المتجه الثاني الذي يكون على رأس المتجه السابق وهذه المتتابعة ترسم بسهم يشير إلى ذيل المتجه السابق أو الأول وهكذا حتى يكون في النهاية الجمع وحاصله هو المتجه الأخير الذي يتم رسمه وهو المتجه المجمع في النهاية بينما تخضع مقادير المتجهات كلها للخاصية التبديلية والترابطية للمجموع.
5-التساوي في المقدار
هذا التساوي بين المتجهات في الطول والمقدار وذلك مثلاً أننا نقول أن متّجه يشير سهمه إلى الشمال ومقداره محدد وواضح فإن المتجه الثاني يساويه في المقدار المحدد وإلى اتجاه الشمال أيضاً فإذا اختلفا في المقدار فإن هذا الاختلاف ينسحب في الاتجاه الشمالي الذي يمكن أن ينحرف قليلاً نحو الشمال الشرقي أو اي اتجاه آخر وفي تلك الحالة فإن التساوي لن يكون موجوداً سواء في المقدار أو في الاتجاه.
6-تختلف عمليات الضرب بين المتجهات
هناك بعض أنواع عمليات الضرب الحديث بين المتجهات حيث يمكن شرب المتجهين ضرباً من خلال النقاط حيث تنتج كميّة قياسية وذلك من خلال الضرب بالضرب بطريقة قياسية بحتة في المقابل فإن ضرب المتجهين لا يتم إلا من خلال الضرب التقاطعي.

خاتمة بحث عن المتجهات

إلى هنا نكون قد وصلنا إلى خاتمة المقال، عدما تناولنا بحث عن المتجهات في الفراع نكون قد تعرفنا على تعريف المتجهات و فوائدها و إستخدامها و بعض الحقائق المثيرة عنها وحتى الخصائص العامة للمتجهات.