تعريف المتجهات كذلك سنذكر ما هي أنواع المتجهات كما سنتحدث عن ضرب المتجهات وأخيرا نسشرح كيفية جمع وطرح المتجهات كل تلك الموضوعات تجدونها من خلال مقالنا هذا.
محتويات المقال
تعريف المتجهات
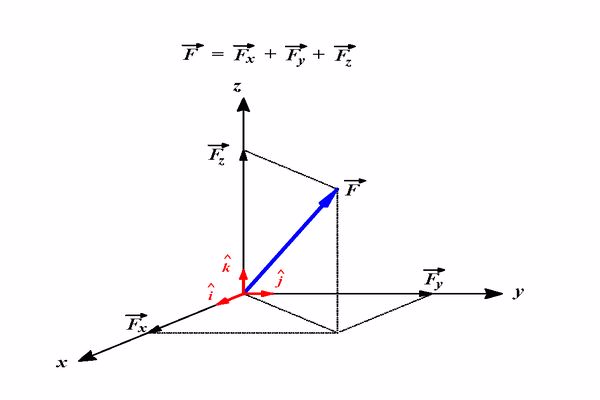
-المتجهات عبارة عن تمثيلات هندسية للحجم والاتجاه والتي يتم تمثيلها غالبًا بأسهم مستقيمة ، تبدأ من نقطة واحدة على محور إحداثيات وتنتهي عند نقطة مختلفة ، جميع المتجهات لها طول ، يُطلق عليه المقدار ، والذي يمثل نوعًا ما من الفائدة بحيث يمكن مقارنة المتجه مع متجه آخر ، المتجهات كونها سهام ، لها أيضًا اتجاه ، هذا ما يميزهم عن العددية ، وهي مجرد أرقام بدون اتجاه ، وتستخدم في العديد من التطبيقات مما يجعل اهمية المتجهات في حياتنا كبيرة.
-يتم تعريف المتجه من خلال حجمه واتجاهه فيما يتعلق بمجموعة من الإحداثيات ، غالبًا ما يكون مفيدًا في تحليل المتجهات لتقسيمها إلى الأجزاء المكونة لها ، بالنسبة للمتجهات ثنائية الأبعاد ، تكون هذه المكونات أفقية ورأسية ، بالنسبة للمتجهات ثلاثية الأبعاد ، يكون عنصر المقدار هو نفسه ، ولكن يتم التعبير عن مكون الاتجاه بدلالة xx و yy و zz.
-وبالتالي من حيث التعريف ، فإن المتجه هو كمية تتميز بالحجم والاتجاه ، ومن أشهر الأمثلة على ذلك هي القوة ، السرعة ، والوزن ، وتعتبر القوة متجه لأن القوة هي مقدار الشدة أو القوة المطبقة في اتجاه ما ، والسرعة هي المتجه حيث تكون سرعته هي المقدار الذي يتحرك فيه كائن في مسار معين.
أنواع المتجهات
يتم تحديد أي متجه من خلال ثلاث عناصر هم: المقدار، والاتجاه، ونقطة التأثير.
1-تشمل أنواع المتجهات ما يلي: المتجه الصفّي، وهو المتجه الذي يتكون من صف واحد.
2-المتجه في الرياضيات عبارة عن سهم ينطلق من نقطة إلى نقطة أخرى.
3-المتجه العمودي، وهو المتجه المكون من عمود واحد.
ضرب المتجهات
1-الضرب العرضي للمتجهات
حاصل الضرب العرضي أو المتجه للمتجهين a و b، المكتوبين a × b ، هو المتجة n×|a|b|sin(a.b)، حيث n هو متجه طول الوحدة عموديًا على مستوى a و b ويتم توجيهه بحيث يتقدم المسمار الأيمن المدور من a نحو b في اتجاه n، وإذا كان a و b متوازيان، فإن a × b = 0، و يمكن تمثيل حجم a × b بمساحة متوازي الأضلاع التي بها a و b كضلع متجاور أيضًا، نظرًا لأن الدوران من b إلى a عكس ذلك من a إلىb.
2-الضرب القياسي للمتجهات
حاصل الضرب القياسي أو النقطي للمتجهين a و b، المكتوب a · b، هو رقم حقيقي | a |*| b *| كوساين (أ ، ب)، حيث (أ ، ب) تشير إلى الزاوية بين اتجاهات أ و ب . إذا كان a و b في زاويتين قائمتين، فإن a · b = 0 ، وإذا لم يكن a و b متجهًا صفريًا، فإن تلاشي حاصل الضرب النقطي يوضح أن المتجهات متعامدة، وإذا كانت a = b فإن cos (a، b) = 1 و a · a = | a | 2 يعطي مربع طول a، والقوانين الترابطية والتبادلية والتوزيعية للجبر الأولي صالحة لمضاعفة النقاط للمتجهات.
جمع وطرح المتجهات
1-طرح المتجهات
و المتجهات تقبل الطرح كذلك ، و كما فعلنا في عملية جمع المتجهات يمكننا العمل في الطرح ، و لكن مع ملاحظة انه عملية الطرح هى نفسها عملية الجمع و لكن لن نقوم بعملية جمع متجهين كما فعلنا في عملية جمع المتجهات و لكن في عملية الطرح سوف نقوم بإضافة المتجه الأول إلى سالب المتجه الثاني ، أي أننا نقوم بإضافة المتجه الثاني و لكن بعدما نقوم بعكس اتجاه هذا المتجه
2-جمع المتجهات
تقبل المتجهات الجمع و يمكننا جمع المتجهات من خلال جمع مركبات المتجه مع بعضها البعض ، حيث نقوم بجمع المركب السيني و المركب الصادي و المركب العيني مع بعضها كل على حدة ، كما انه يوجد طريقة هندسية أيضا لجمع المتجهات و ذلك من خلال تمثيل المتجه الأول ثم نقوم بوضع ذيل المتجه الثاني على رأس المتجه الأول و هكذا و في النهاية نقوم برسم سهم من ذيل المتجه الأول إلى رأس المتجه الثاني ، و هذا المتجه الأخير الذي قمنا برسمه هو حاصل عملية الجمع ويسمى المتجه المحصل ، و يتميز جمع المتجهات بخصائص الجمع التبديلية و الترابطية .