جمع وطرح المتجهات نتحدث عنها من خلال مقالنا هذا كما نذكر لكم تاريخ المتجهات و جمع متجهين بالرسم البياني ومركّبات المتّجهات وختام الموضوع مفهوم الكميات المتجهة تابعوا السطور القادمة.
محتويات المقال
جمع وطرح المتجهات
جمع المتجهات:
يمكن جمع المتجهات عن طريق جمع مُركّبات المتّجه معاً؛ أي جمع المركبات السينيّة، وجمع المركبات الصاديّة، وجمع المركبات العينيّة كلٌّ على حِدة، أو يمكن جمع المتجهات بطريقة هندسيّة؛ بحيث يوضَع المتجه الأول ثمّ يوضَع ذيل المتجه الثاني على رأس الأول، وهكذا، وفي النهاية يُرسَم سهم من ذيل المتجه الأول إلى رأس الأخير، ويكون حاصل الجمع هو هذا المتجه الأخير الذي تمّ رسمه، وهو ما يُعرَف بالمتجه المُحصّل، ويخضع جمع المتجهات للخاصيّتين التبديليّة والترابطيّة للجمع.
طرح المتّجهات:
عمليّة الطرح في المتجهات هي نفسها عمليّة الجمع، ولكن بدل جمع متّجهين فإنّه تتمّ إضافة المتجه الأول إلى سالب المتجه الثاني؛ أي إضافة المتجه الثاني بعد عكس اتجاهه.
تاريخ المتجهات
-مر مفهوم المتجهات بمراحل كثيرة من التطور حتى نراه بشكله المعاصر ، و على مدار 200 عام قدم العديد من العلماء الكثير من المساهمات في تطوير مفهوم المتجهات ، حيث قام ” Giusto Bellavita ” بتجريد و توضيح الفكرة الرئيسية الأطروحة في عام 1935 عندما قام بتأسيس مفهوم ” equipollence ” ، و قام العالم ويليام روان هاميلتون فيما بعد بتقديم مصطلح المتجهات ، و قام العديد من العلماء على رأسهم هيرمان جراسمان و كونت دي سان و أوغسطين كوشي و ماثيو أوبراين و أغسطس موبيوس بتطوير عدة انظمة مشابهة للنواقل في منتصف القرن التاسع عشر.
-حيث قام جروسمان في عام 1840 بوضع نظرية الانحراف و التي تعد أول الانظمة التحليلية المكانية التي تشابه نظام اليوم ، و في عام 1878 قام ويليام كينجدون كليفورد بنشر عناصر ديناميكية و قام بتبسيط بعض الدراسات التي سبقته ، و قام إدوين بيدويل ويلسون في عام 1901 بنشر تحليل المتجهات و الذي تمت له عملية تعديل من محاضرات جيب و التي قامت بنفي أي ذكر لقضية التأخر في عملية تطوير المتجهات في حساب التفاضل و التكامل .
جمع متجهين بالرسم البياني
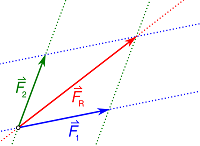
نفترض أن متجهين تؤثر على جسم. يمكننا بواسطة الرسم البياني تعيين المحصلة، كالآتي:
1-نرسم المتجهين كسهمين بمقياس رسم معين، من حيث المقدار والاتجاه.
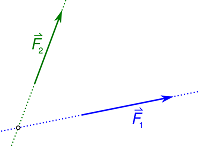
2-نرسم من رأس السهم الأول خطا موازيا للسهم الثاني،
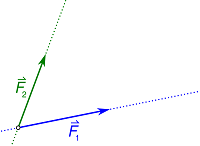
3-ونرسم من رأس السهم الثاني خطا موازياً للسهم الأول. يتقاع الخطان ويكتمل متوازي الأضلاع.
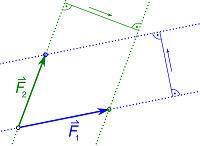
4-المحور الباديء من نقطة تأثير المتجهين إلى نقطة تقاطع الخطين هي محصلة المتجهين، وتقوم مقامهما.
مركّبات المتّجهات
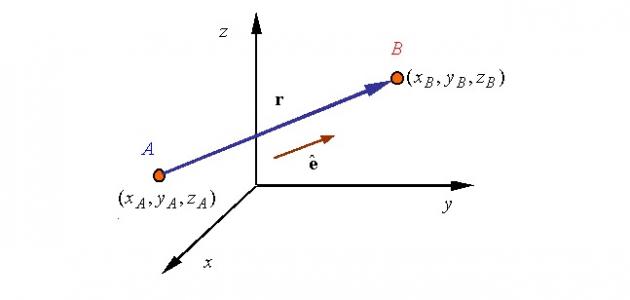
-لأيّ مُتّجه توجد مُركبات تعتمد على نظام الإحداثيات الذي نحن فيه، وفي هذا المقال سيتمّ تناول نظام الإحداثيات الديكارتي، يمكن التعبير عن جميع المتجهات في المستوى الديكارتي من خلال مركبات سينيّة وصاديّة وعينيّة، حيث إنّ أي متجه يساوي مجموع هذه المركبات الثلاثة، أي المركبة السينيّة مضروبةً بمتجه الوحدة السينيّ، والمركبة الصاديّة مضروبة بمتجه الوحدة الصادي، والمركبة العينيّة مضروبة بمتجه الوحدة العيني، والمركبة هي تعبير عن طول المتجه على محاور نظام الإحداثيات المستخدم، فيمكن القول إنّ طول المتجه على محور السينات يساوي المركبة السينيّة لهذا المتجه، والأمر نفسه فيما يخصّ المركبتين الصاديّة والعينيّة.
– كما ذُكِر سابقاً فإنّ متجه الوحدة يظهر عند التعبير عن المتجهات باستخدام المركبات، ويمكن تعريف متجه الوحدة على أنّه متجه عديم الأبعاد مقداره واحد، واتجاهه يُعبّر عن اتجاه كل مركبة من مركبات المتجه، وتخلتف متجهات الوحدة باختلاف نظام الإحداثيات المُستخدَم، ولو كان لدينا متجه في المستوى السيني والصادي فقط، ولو كانت الزاوية بين محور السينات والمتجه هي (φ)، فإنّ مقدار المركبة السينيّة سيكون مساوياً لطول هذا المتّجه مضروباً بجيب التمام للزاوية (φ)، وطول المركبة الصاديّة سيكون مساوياً لطول المتجه مضروباً بجيب الزاوية (φ).
مفهوم الكميات المتجهة
-المتجه في الفيزياء، هو كمية لها مقدار واتجاه، ويتم تمثيله عادةً بواسطة سهم يكون اتجاهه هو نفس اتجاه الكمية ويكون طوله متناسبًا مع حجم الكمية، وعلى الرغم من أن المتجه له مقدار واتجاه، إلا أنه ليس له موضع، أي أنه طالما لم يتغير طوله، فلا يتم تغيير المتجه إذا تم إزاحته بالتوازي مع نفسه.
-على عكس المتجهات تسمى الكميات العادية التي لها حجم ولكن ليس اتجاهًا كميات قياسية، وعلى سبيل المثال الإزاحة والسرعة والتسارع هي كميات متجهة، في حين أن السرعة (مقدار السرعة) والوقت والكتلة هي كميات قياسية.
-للتأهل كمتجه، يجب أن تمتثل الكمية التي لها حجم واتجاه أيضًا لقواعد معينة للجمع، واحدة من هذه هي إضافة ناقلات، مكتوبة بشكل رمزي كـ A + B = C (يتم كتابة المتجهات بشكل تقليدي كأحرف غامقة)، وهندسيًا يمكن تصور مجموع المتجه عن طريق وضع ذيل المتجه B على رأس المتجه A ورسم المتجه C بدءًا من ذيل A وينتهي عند رأس B – بحيث يكمل المثلث.
-إذا كانت A و B و C متجهات، فيجب أن يكون من الممكن إجراء نفس العملية وتحقيق نفس النتيجة (C) بترتيب عكسي، B + A = C، وتمتلك الكميات مثل الإزاحة والسرعة هذه الخاصية (قانون التبادل)، ولكن هناك كميات (على سبيل المثال، دوران محدود في الفضاء) لا تكون متجهة، وبالتالي فهي ليست نواقل.
-القواعد الأخرى لمعالجة المتجهات هي الطرح والضرب بواسطة العددي والضرب القياسي (المعروف أيضًا باسم المنتج النقطي أو المنتج الداخلي) وضرب المتجه (المعروف أيضًا باسم الضرب المتقاطع) والتفاضل، لا توجد عملية تقابل القسمة على متجه.