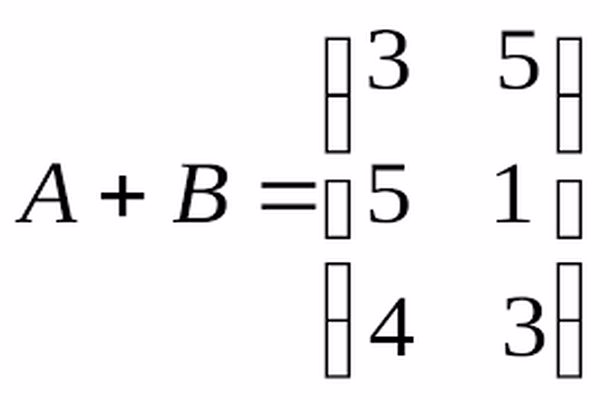خصائص المصفوفات كذلك سنتحدث عن أهمية المصفوفات أيضا سنذكر ما هي أنواع المصفوفات وكذلك أهم تعاريف خاصة بالمصفوفات كل تلك الموضوعات تجدونها من خلال مقالنا هذا
محتويات المقال
خصائص المصفوفات
1-قانون الجمع
لدينا ثلاث مصفوفات A = [a ij]، B = [b ij]، C = [c ij] لهما نفس الترتيب وهو m × n، (A + B) + C = A + (B + C).
2-قانون التبادل
إذا كان A = [a ij]، B = [b ij] لهما نفس الترتيب والحجم هو m × n، ثم A + B = B + A. فيمكن أن يتم التبادل بين المصفوفات في الجمع.
3-الهوية المضافة
لنفترض أن A = [a ij] مصفوفة m × n وO تكون مصفوفة m × n صفرية، ثم A + O = O + A = A. فتعتبرO هي الهوية المضافة لجمع المصفوفة.
3-المعكوس الإضافي
مثلا لدينا A = [a ij] m × n أي مصفوفة، ومصفوفة أخرى مثل – A = [–a ij] m × n بحيث تكون A + (–A) = (–A) + A = O. – A هو المعكوس الجمعي لـ A أو سالبA.
أهمية المصفوفات
1- تُعد المصفوفات من أكثر الأمور المستخدمة في كثير من التطبيقات العلمية مثل الفيزياء، والمجالات البصرية، والهندسية.
2- وتُستخدم أيضًا في نظريات الاحتمالات المختلفة، والإحصاء وتُستخدم في التعبير عن الكثير من الأنظمة الاقتصادية.
3-تدخل في دراسة الكثير من الظواهر الفيزيائية، كما يتم استخدامها في كثير الرسومات خصوصًا ذات البعد الثلاثي.
4-الرسومات على الكمبيوتر في حلول الخوارزميات وترتيب الصفحات.
5-تستخدم في معالجة الكثير من التحولات الخطية لعرض الصور.
6-الكثير من المجالات الأخرى المهمة.
7-فهم المفاهيم الخاصة بالتحليلية الكلاسيكية مثل الدلات الأسية والمشتقات بأبعاد عالية.
ما هي أنواع المصفوفات
1-مصفوفة الوحدة (unit matrix)
وهي مصفوفة مربعة أيضاً وجميع عناصر صفوفها وأعمدتها تأخذ القيمة (صفر) ما عدا عناصر القطر الرئيسي فيأخذ القيمة (1) وهذا هو أساس الإختلاف بينها وبين المصفوفة القطرية ويرمز لها بالرمز (I) مثلا
2-المصفوفة المتماثلة (Symmetric matrix)
إذا كان هناك مصفوفة مربعية (أ (م × ق)) وتم إستبدال عناصر صفوفها بعناصر أعمدتها بنفس الترتيب أصبحت مصفوفة مبدلة (أ′ (م × ق)) وإذا لم تتغير قيم العناصر المتناظرة في كل منها عن الأخرى بعد الإجراء السابق فيطلق على مثل هذه المصفوفة بالمصفوفة المتماثلة. ومن الممكن أن تتم ملاحظة على مثل هذه المصفوفة أيضاً هو أن العناصر المتناظرة فيها أعلى وأسفل القطر الرئيسي تكون متماثلة.
3- مصفوفة المتجهات (vectors matrix)
وهي مصفوفة تتكون من صف واحد وعدة أعمدة وفي هذه الحالة يسمى متجة صف (Row vector) في حين لو تكونت هذه المصفوفة من عمود واحد وعدة صفوف سمى متجه عمود(Celumn vector)
4- المصفوفة الشاذة أو المنفردة (Singular matrix)
وهي مصفوفة مربعة نجد أن محدد عناصرها = صفر فمثلاً: لكن إذا كان محدد المصفوفة ≠ صفر فيطلق عليها مصفوفة غير شاذة أو غير منفردة.
5-المصفوفة المبدلة (Transpose matrix)
إذا كان لدينا مصفوفة (أ (م × ق)) أي عدد صفوفها (م) وعدد أعمدتها (ق)، وتم استبدال عناصر الصفوف بعناصر الأعمدة بنفس الترتيب أو العكس فإن المصفوفة الجديدة ولتكن (أ′) يطلق على هذه المصفوفة (أ′ (م × ق) بالمصفوفة المبدلة.
6- المصفوفة القياسية (Scarler Matrix)
وهي عبارة عن مصفوفة واحدة (I)، مضروب عناصر قطرها الرئيسي × رقم قياسي محدد، وينتج عن ذلك المصفوفة القياسية ونلاحظ أن عناصر القطر الرئيسي متساوية في القيمة.
7-المصفوفة المستطيلة
وهي المصفوفة التي عدد صفوفها لا يساوي عدد أعمدتها وقد يكون م > ق أو م < ق.
8-المصفوفة الصفرية
إذا كانت كافة عناصر المصفوفة (سواء كانت مستطيلة أو مربعة) تأخذ القيمة (صفر) فيطلق عليها المصفوفة الصفرية. المصفوفة القطرية (Diagonal matrix): وهي مصفوفة مربعة جميع عناصرها تأخذ القيمة (صفر) ما عدا عناصر القطر الرئيسي، وهو القطر الذي يبدأ من الشمال الشرقي إلى الجنوب الغربي للمصفوفة فيأخذ قيماً لا تساوي الصفر وتختلف كلها أو بعضها في القيم الحسابية
تعاريف خاصة بالمصفوفات
1-معكوس مصفوفة
هو المعكوس الضربي للمصفوفة بحيث يكون حاصل ضرب المصفوفة في معكوسها يساوي مصفوفة الواحد أي B = In وتدعى المصفوفة B مقلوب A ورمزها A-1 .4
2-المتّجه
هو المصفوفة المؤلفة من صفٍ واحدٍ وعمودٍ واحدٍ، حيث أن المصفوفة ذات العمود الواحد يُرمز لها بالشكل Am*1 وتعرف باسم متجه عمودي، بينما المصفوفة المؤلفة من صف واحد يُرمز لها ب A1*n وتعرف باسم متجه صفي.
3-منقول مصفوفة
منقول مصفوفة: هو المَصفوفة الناتجة عن تبديل الأعمدة بالأسطر ويرمز لها AT ومن خواصها أن منقول مجموع مصفوفتين هو مجموع منقول مصفوفتين أي (A+B)T = AT+BT ، وأيضًا منقول حاصل ضرب مصفوفتين هو حاصل ضرب المصفوفتين بشكلٍ معاكسٍ لمنقولهما أي ( A.B)T = BT*AT
4-حيّز المصفوفة أو رتبتها أو قياسها
يعرّف بأنه عدد الأسطر في جداء عدد الأعمدة؛ أي إذا كان لدينا مصفوفة تحتوي على 5 أسطر و 3 أعمدة فإن قياسها أو رتبتها هو 3*5 .