درس المتجهات في الفضاء نتحدث عنها من خلال مقالنا هذا كما نذكر لكم باقة متنوعة أخرى من المعلومات عن المتجهات مثل بعض خصائص المتجهات ومميزات المتجهات ومركّبات المتّجهات .
محتويات المقال
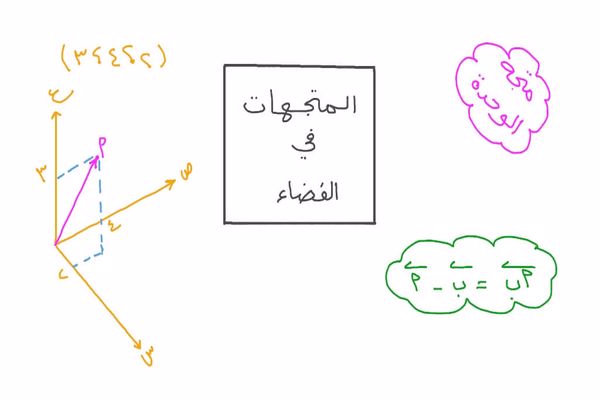
درس المتجهات في الفضاء
تعريف المتجهات في الفضاء الثلاثي الابعاد
يعرف المتجه بأنه كمية لها مقدار واتجاه وهندسيًا، يمكننا أن نتخيل متجهًا على شكل قطعة مستقيمة موجهة، طولها هو مقدار المتجه، وفي نهايتها سهم يشير إلى الاتجاه؛ حيث يكون اتجاه المتجه من ذيله إلى رأسه. ويكون المتجهان متماثلان إن كان لهما نفس الحجم والاتجاه، هذا يعني أنه إذا أخذنا متجهًا وقمنا بنقله إلى موضع جديد مع بقائه في نفس الاتجاه، فإن المتجه الذي سنحصل عليه في نهاية هذه العملية هو نفس المتجه الذي كان لدينا في البداية. ومن الأمثلة على المتجهات متجهي القوة والسرعة؛ فكل من القوة والسرعة يكونان في اتجاه معينًا أما طول المتجه فيشير إلى مقدار القوة أو مقدار السرعة.
شرح المتجهات في الرياضيات
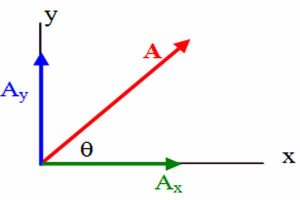
أول ما يجب عليك أن تتعلمه هو أن المتجه يرمز له بحرف انجليزي وفوق سهم كهذا ( → )، أما الكمية القياسية فنرمز له فقط بحرف من دون سهم فوقه، وفي الصورة التالية يمكنك أن تلحظ أن المتجه المرموز له بالحرف (A) متجه موجود في بعدين اثنين، وهنا سوف أبدأ بالشرح لك عن المتجه في بعدين نظرًا لسهولة هذا الموضوع، فهنا المتجه A يمكن تحليله إلى مركبتين من عمل اسقاط عمودي على كل من المحورين السيني والصادي لنحصل على مسقط رأسي ومسقط أفقي، ونرمز لهما على الترتيب بالرمزين ( AY ، AX)؛ بحيث يمكننا أن نكتب المتجه بطريقتين الأولى عن طريق كتابة مركباته والثانية من خلال كتابة المقدار والزاوية ومن الشكل الهندسي السابق نستنتج أن المتجه A يمكن أن نكتبه كالتالي: ( A=AY+AX)، أما الطريقة الثانية فتكون من خلال كتابة المقدار ويليه الزاوية كما يأتي: ( A ∠θ ). مع ملاحظة أننا أهملنا وضع السهم فوق الكميات المتجهة لصعوبة ذلك.
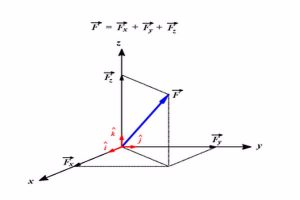
لعلك تلاحظ أن الصورة في الأعلى تمثل متجه موضوع في الأبعاد الثلاثة، ويمكنك أن تكتبه بالطريقة نفسها التي ذكرناها سابقًا من خلال اسقاط المتجه على المركبات الثلاثة ( X، Y، Z)، بحيث يكون البعد الثالث هو البعد الداخل في العمق وهو ( Z )، وبالتالي يمكنك أن تكتب المتجه بالطريقة الآتية: ( A= AX+AY+AZ) ويمكننا تلخيص ما سبق كالتالي؛ لكتابة المتجهات في ثلاثة أبعاد يتطلب هذا ثلاثة محاور عمودية متبادلة، وعادةً ما يتم عرض المحورين x و y أفقيًا والمحور z عموديًا، كما يمكن تحديد موضع النقطة التي يصل إليها سهم المتجه باستخدام ثلاثة إحداثيات (x ، y ، z)، ويكون الأصل O مُعطى بواسطة الاحداثيات (0 ، 0 ، 0) لهذه النقطة.
بعض خصائص المتجهات
1-ضرب المتجهات
المتجهات كميات تقبل الضرب كذلك ، حيث يمكننا ان نقوم بضرب متجه ما بكمية قياسية ، و عملية ضرب متجه بكمية قياسية هي عبارة عن تغيير في طول المتجه أي أننا في عملية الضرب نقوم بتغيير مقدار المتجه و لكن اتجاهه لن يتغير لو تم ضربه في أي رقم و اما عن ضرب المتجهات في بعضها البعض فإنه يوجد نوعين من ضرب المتجهات حيث أنه لو قمنا بضرب متجهين من خلال الضرب النقطي فإن الناتج من هذه العملية سوف يكون عبارة عن كمية قياسية و لذلك فإن هذا النوع من الضرب يعرف الضرب القياسي ، أما النوع الثاني من ضرب المتجهات فإنه يسمى الضرب الاتجاهي و فيه تقوم بضرب المتجهين ضربا تقاطعوا والناتج هنا يكون متجها جديد عمودي على المتجهين الذين قمنا بضربهما.
2-تساوي المتجهات
إذا وجد متجهان لهما نفس الطول و المقدار و يكون متجهين إلى نفس الاتجاه أي يشيران إلى اتجاه واحد فإن هذان المتجهان يكونون في هذه الحالة متساويين ، و مثالا على تساوي المتجهات يمكننا القول أن هناك متجهين يشيران إلى الجنوب و مقدار كل متجه منهما 5 إذن يمكننا القول إن هذان المتجهان متساويان ، أما لو كان لأحد المتجهات مقدار مختلف عن الآخر أو انه يشير إلى اتجاه مختلف عن الآخر فإن هذين المتجهين لن يكونا متساويين.
3-طرح المتجهات
المتجهات تقبل الطرح كذلك ، و كما فعلنا في عملية جمع المتجهات يمكننا العمل في الطرح ، و لكن مع ملاحظة انه عملية الطرح هى نفسها عملية الجمع و لكن لن نقوم بعملية جمع متجهين كما فعلنا في عملية جمع المتجهات و لكن في عملية الطرح سوف نقوم بإضافة المتجه الأول إلى سالب المتجه الثاني ، أي أننا نقوم بإضافة المتجه الثاني و لكن بعدما نقوم بعكس اتجاه هذا المتجه.
4-جمع المتجهات
تقبل المتجهات الجمع و يمكننا جمع المتجهات من خلال جمع مركبات المتجه مع بعضها البعض ، حيث نقوم بجمع المركب السيني و المركب الصادي و المركب العيني مع بعضها كل على حدة ، كما انه يوجد طريقة هندسية أيضا لجمع المتجهات و ذلك من خلال تمثيل المتجه الأول ثم نقوم بوضع ذيل المتجه الثاني على رأس المتجه الأول و هكذا و في النهاية نقوم برسم سهم من ذيل المتجه الأول إلى رأس المتجه الثاني ، و هذا المتجه الأخير الذي قمنا برسمه هو حاصل عملية الجمع ويسمى المتجه المحصل ، و يتميز جمع المتجهات بخصائص الجمع التبديلية و الترابطية.
مميزات المتجهات
1-قد تعمل على التمييز بين الكميات المتجهة والكميات السلمية التي يطلق عليها الكميات العددية والكميات القياسية.
2- تقوم الكمية المتجهة بتصنيف الكميات الفيزيائية إلى كميات عددية وكميات متجهة، وقد يتم التمثيل إلى هذه المتجهات من خلال الرسم، ويتم تحليل هذه المتجهات في العديد من المستويات التي تحتوي على محورين متعامدين، لإيجاد قيمة خاصة بالمتجهات التي يتم التعرف عليها من خلال المركبات السينية والصادية الخاصة به.
3- تتميز بتوفير إمكانية الجهات الخاصة بالعقار.
4-قد تجرى هذه العملية التي لها علاقة بالمتجهات للعمليات الحسابية الأساسية.
5- يساعد هذا التطبيق بالعمل على إدراك الفرق بين الكميات السليمة والكميات المتجهة.
مركّبات المتّجهات
-لأيّ مُتّجه توجد مُركبات تعتمد على نظام الإحداثيات الذي نحن فيه، وفي هذا المقال سيتمّ تناول نظام الإحداثيات الديكارتي، يمكن التعبير عن جميع المتجهات في المستوى الديكارتي من خلال مركبات سينيّة وصاديّة وعينيّة، حيث إنّ أي متجه يساوي مجموع هذه المركبات الثلاثة، أي المركبة السينيّة مضروبةً بمتجه الوحدة السينيّ، والمركبة الصاديّة مضروبة بمتجه الوحدة الصادي، والمركبة العينيّة مضروبة بمتجه الوحدة العيني، والمركبة هي تعبير عن طول المتجه على محاور نظام الإحداثيات المستخدم، فيمكن القول إنّ طول المتجه على محور السينات يساوي المركبة السينيّة لهذا المتجه، والأمر نفسه فيما يخصّ المركبتين الصاديّة والعينيّة.
– كما ذُكِر سابقاً فإنّ متجه الوحدة يظهر عند التعبير عن المتجهات باستخدام المركبات، ويمكن تعريف متجه الوحدة على أنّه متجه عديم الأبعاد مقداره واحد، واتجاهه يُعبّر عن اتجاه كل مركبة من مركبات المتجه، وتخلتف متجهات الوحدة باختلاف نظام الإحداثيات المُستخدَم، ولو كان لدينا متجه في المستوى السيني والصادي فقط، ولو كانت الزاوية بين محور السينات والمتجه هي (φ)، فإنّ مقدار المركبة السينيّة سيكون مساوياً لطول هذا المتّجه مضروباً بجيب التمام للزاوية (φ)، وطول المركبة الصاديّة سيكون مساوياً لطول المتجه مضروباً بجيب الزاوية (φ).