كيف نحسب محيط المستطيل

كيف نحسب محيط المستطيل، ومسائل على محيط المستطيل، وخصائص المستطيل، ونصائح لتحسين المهارات في مادة الرياضيات، نتناول الحديث عنهم بشيء من التفصيل خلال المقال التالي.

كيف نحسب محيط المستطيل

أولًا: قانون محيط المستطيل
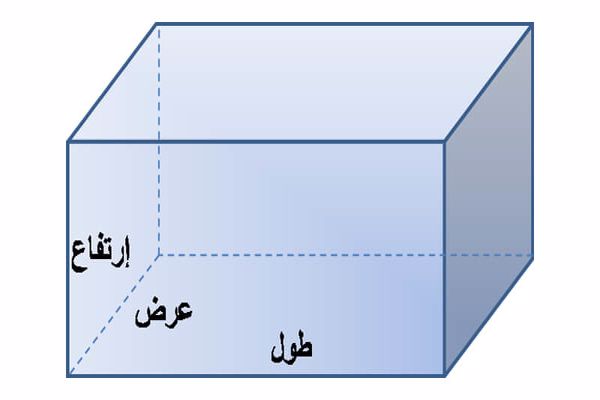
محيط المستطيل هو مجموع أطوال أضلاعه، حيث يعرف المستطيل كشكل رباعي أو شكل هندسي بأربعة أضلاع به كل ضلعين متقابلين متطابقين، مما يعني أن لهما نفس الطول، كما أن ليس كل مستطيل مربع لكن يمكن اعتبار كل مربع مستطيل أو شكلًا مركبًا من المستطيلات.
ثانيًّا: طرق حساب المحيط
– إيجاد المحيط باستخدام الطول والعرض
1. اكتب المعادلة الأساسية
لإيجاد محيط المستطيل، ستساعد هذه المعادلة في إرشادك عند حساب محيط المستطيل. المعادلة الأساسية هي: المحيط = 2 (الطول + العرض).
المحيط دومًا هو المسافة الكلية بامتداد الحواف الخارجية لأي شكل، سواءً كان بسيطًا أم مركبًا.
سنرمز للمحيط في هذه المعادلة ب رمز “م” و”ط” لطول المستطيل و”ع” لعرضه.
قيمة الطول أكبر من العرض دومًا.
سيتساوى الطولان والعرضان في المستطيل نظرًا لتساوي الأضلاع المتقابلة. هذا سبب كتابتنا للمعادلة كعملية ضرب لمجموع الطول والعرض في 2.
كما يمكنك كتابة المعادلة م = ط + ط + ع + ع لتوضيح هذه المسألة أكثر.
2. جد طول المستطيل وعرضه
ستعطى طول المستطيل وعرضه في المسألة بالنسبة لمسائل الرياضيات البسيطة؛ عادة ما توضح هذه القيم بجوار رسم المستطيل.
استخدم مسطرة أو عصا أو شريط قياس لإيجاد طول وعرض المساحة التي تحاول حسابها إذا كنت تحسب محيط مستطيل في الواقع، قس كل الأضلاع إذا كنت خارج البيت لترى ما إذا كانت الأضلاع المتقابلة تتطابق حقًا.
مثال: الطول = 14 سم والعرض = 8 سم.
3. جمع الطول والعرض
عليك أن تعوض بقيم الطول والعرض في المعادلة بعد تحديدها.
لاحظ عند حل معادلات المحيط أن العمليات الموجودة داخل الأقواس المربعة أو العادية تحل قبل الموجودة خارجها وفقًا لأولوية العمليات، لهذا ستبدأ بحل المعادلة بجمع الطول والعرض.
على سبيل المثال: المحيط = 2* (الطول + العرض) = 2 (14 + 8) = 2*22.
4. ضرب مجموع الطول والعرض في 2
يضرب (الطول + العرض) في 2 عند النظر لمعادلة إيجاد محيط المستطيل وستحصل على المحيط حين تتم عملية الضرب هذه.
تأخذ عملية الضرب هذه في الحسبان ضلعي المستطيل الآخرين، لقد جمعت ضلعين فقط من الشكل عند جمع الطول والعرض.
يمكنك ضرب الناتج في 2 لإيجاد مجموع كل الأضلاع نظرًا لتساوي جانبي المستطيل الآخرين مع الجانبين المجموعين.
على سبيل المثال: المحيط = 2 * (الطول + العرض) = 2 *(14+8) = 2*22 = 44 سم.
5. اجمع “الطول + الطول + العرض + العرض”
يمكنك جمع الأضلاع الأربعة معًا مباشرة لإيجاد محيط المستطيل بدلًا من جمع ضلعين وضرب الناتج في 2.
هذه نقطة بداية رائعة إذا كنت تجد صعوبة في مفهوم المحيط.
على سبيل المثال: المحيط = الطول +الطول +العرض + العرض = 14 + 14 + 8 + 8 = 44 سم.
– حساب المحيط بمعرفة المساحة وأحد الأضلاع
1. اكتب معادلة مساحة المستطيل ومعادلة محيطه.
أنت تعرف مساحة المستطيل في هذه المسألة، لكن لا يزال عليك استخدام معادلتها لإيجاد المعطيات الناقصة.
مساحة المستطيل هي حساب المساحة ثنائية الأبعاد الواقعة داخل حدود المستطيل أو عدد الوحدات المربعة داخله.
المعادلة المستخدمة لإيجاد المساحة هي س = ط * ع.
المعادلة المستخدمة لإيجاد المحيط هي م = 2* (ط + ع).
ترمز “س” في المعادلة أعلاه للمساحة و”م” للمحيط و”ط” للطول و”ع” للعرض.
2. اقسم المساحة الكلية على طول الضلع الذي تعرفه
سيمكنك هذا من إيجاد طول الضلع المجهول للمستطيل سواءً كان طولًا أم عرضًا؛ حينها سيمكنك إيجاد هذه المعلومة الناقصة من حساب المحيط.
ستعطيك قسمة المساحة على العرض الطول لأنك تضرب الطول في العرض لإيجاد المساحة. بالمثل، سنحصل على العرض من قسمة المساحة على الطول.
على سبيل المثال: س = 112 سم مربع وط = 14 سم.
س = ط*ع
112 = 14*ع
112/14 = ع
ع = 8
3. اجمع الطول والعرض
يمكنك الآن بعد أن أصبحت تعرف أبعاد المستطيل طولًا وعرضًا أن تعوض بهما في معادلة محيط المستطيل.
س تجمع الطول العرض أولًا في هذه المسألة لأن هذا الجزء من المعادلة داخل الأقواس.
عليك أن تحسب الجزء الموجود داخل الأقواس أولًا دومًا حسب أولوية العمليات الحسابية.
4. اضرب مجموع الطول والعرض في 2
يمكنك إيجاد محيط المستطيل بعد جمع الطول والعرض بضرب الناتج في 2. يأخذ هذا في الحسبان ضلعي المستطيل الآخرين.
ستتمكن من إيجاد محيط المستطيل بجمع الطول والعرض وضرب الناتج في 2 نظرًا لتساوي أطوال الأضلاع المتقابلة.
يتساوى الطولان في المستطيل وكذلك العرضان.
على سبيل المثال: المحيط = 2 * (14 + 8) = 2* 22 = 44 سم.

مسائل على محيط المستطيل

– مثال 1
أوجد محيط ومستطيل طوله 17 سم وعرضه 13 سم؟
الحل:
معطيات: الطول = 17 سم ، العرض = 13 سم
محيط المستطيل = 2 ( الطول + العرض )
= 2 ( 17 + 13 ) سم
= 2 × 30 سم
= 60 سم
نعلم أن مساحة المستطيل = الطول × العرض
= ( 17 × 13 ) سم2
= 221 سم2
– مثال 2
طول وعرض الفناء المستطيل 75 م و 32 م أوجد تكلفة التسوية بمعدل 3 دولارات لكل متر مربع ، أيضًا ابحث عن المسافة التي قطعها الصبي لأخذ 4 جولات من الفناء.
الحل:
طول الفناء = 75 م
اتساع الباحة = 32 م
محيط الفناء = 2 ( 75 + 32 ) م
= 2 × 107 م
= 214 م
المسافة التي قطعها الصبي في 4 جولات = 4 × محيط الفناء
= 4 × 214 = 856 م
نعلم أن مساحة الفناء = الطول × العرض
= 75 × 32 م2
= 2400 م2
لمسافة 1 م2، تكلفة التسوية = 3 دولارات
2400 م2، تكلفة التسوية = 3 دولار
= 7200 دولار أمريكي

خصائص المستطيل

1. يساوي حاصل جمع الزوايا الداخلية 360 درجة.
2. الأقطار تنصِّف بعضها، وتتساوى بالطول.
3. تكون الزوايا في الأقطار المتناصفة، بعضها حاد والآخر منفرج الزاوية، وفي حال كانت كل الزوايا قائمة فإن الشكل يصبح مربعًا.
4. مستطيل بطول ضلعه a وb، فإن محيطه 2a + 2b، ومساحته a×b.
5. قطر المستطيل هو قطر الدائرة المارّة برؤوسه.
6. في حال كان لدينا كل من الطول a والعرض b، فيمكن التعبير عن القطر بالعلاقة a²+b²)√ يمكننا الحصول على أسطوانة، عبر تدوير المستطيل وذلك عبر محورين:
– محور موازٍ للطول، في هذه الحالة، يكون ارتفاع الأسطوانة مساويًا لعرض المستطيل، كما أن قطر الأسطوانة يعادل طول المستطيل.
– محور موازي للعرض، يساوي ارتفاع الأسطوانة طول المستطيل. وبالمثل، فإن قطرها يعادل العرض.2

نصائح لتحسين المهارات في مادة الرياضيات

1. يجب أولًا تنظيم وقتك وإدارته بشكل صحيح مع ترتيب أولوياتك، ثم تحديد هدفك الذي تريد الوصول إليه، ويجب أن يسأل الطالب ويستفسر عند مواجهته لأي معلومات بها صعوبة في الشرح أثناء عرض الدرس عليه.
2. يجب الفهم والتركيز جيدًا في مادة الرياضيات مع حفظ القوانين المتعلقة بحل المسائل الحسابية، مع التدريب والتمرن المستمر على حل المسائل، واستغلال الوقت أيضًا في الإجازات.
3. تحتاج مادة الرياضيات إلى متابعة ومذاكرة ما تم شرحه أول بأول، وتستلزم الدراسة في مكان هادئ لكي يساعدك على التركيز والتفكير.