ماهي الاعداد الاوليه وماهو تعريفها الصحيح سنتعرف على كل شىء عن الاعداد الاولية من خلال السطور التالية .
محتويات المقال
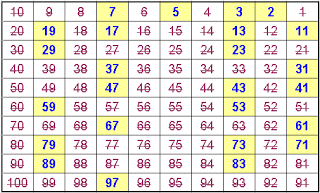
عدد أولي
العدد الأولي والعدد الأول هو عدد طبيعي أكبر قطعاً من 1، لا يقبل القسمة إلا على نفسه وعلى الواحد فقط. يُدعى كل عدد طبيعي أكبر قطعاً من 1 وغير أولي عددا مؤلفا. على سبيل المثال، 5 هو عدد أولي لأنه لا يقبل القسمة إلا على 1 وعلى 5، بينما 6 هو عدد مؤلف لأنه قابل للقسمة على 1، وعلى 2 وعلى 3 وعلى 6. تقيم المبرهنة الأساسية في الحسابيات الدور المركزي للأعداد الأولية في نظرية الأعداد : كل عدد صحيح طبيعي أكبر قطعا من 1 يساوي جداء مجموعة وحيدة ما من الأعداد الأولية (بغض النظر إلي ترتيب هؤلاء الأعداد داخل هاته المجموعة). هاته المبرهنة تستلزم إقصاء 1 من لائحة الأعداد الأولية.
لتحديد أولية عدد ما، توجد طريقة سهلة ولكنها بطيئة، تسمى القسمة المتكررة، وتتمثل في قسمة هذا العدد علي الأعداد المحصورة بين 2 والجذر التربيعي للعدد المعين. توجد خوارزميات أخرى أكثر فعالية من القسمة، تستعمل في تحديد أولية الأعداد الكبيرة، وخصوصا عندما يتعلق الأمر بأعداد ذات شكل خاص كأعداد ميرسين الأولية. بحلول فبراير 2013، تألف أكبر عدد أولي تم الوصول إليه من 17 مليون رقما.
مجموعة الأعداد الأولية مجموعة غير منتهية. وقد برهن على ذلك أقليدس في حوالي عام 300 قبل الميلاد. لا تعرف صيغة ما، جميع قيمها أعداد أولية. ولكن توزيع الأعداد الأولية يمكن أن يخضع للدرس وأن تقام حوله النظريات. أول مبرهنة تذهب في هذا الاتجاه هي مبرهنة الأعداد الأولية، والتي بُرهن عليها في نهاية القرن التاسع عشر والتي بموجبها الاحتمال أن يكون عدد طبيعي ما n، اختير بصفة عشوائية، أوليا، يتناسب عكسيا مع عدد الأرقام التي يحتوي عليها هذا العدد. وبتعبير آخر، يتناسب عكسيا مع اللوغارتم الطبيعي ل n.
إكتشاف أكبر عدد أوليّ
قد إكتشف الدّكتور كيرتس كوبر في جامعة ميسوري في أمريكا عن طريق الحاسب الآليّ أكبر عدد أوليّ ، حيث يتكوّن العدد الذي إكتُشِف من أكثر من 22 مليون رقماً، وهو أكبر من العدد الأوليّ الذي قد إكتُشِفَ قبله بخمسة ملايين رقم تقريباً، والعدد الذي إكتُشِف حتى الآن حاصلٌ على الترتيب التاسع والأربعين في سلسلة أوليّة ميرسيني؛ وتفيد هذه الأرقام الأوليّة الكبيرة جداً في عمليّات الحوسبة للمستقبل؛ لأنّ الأرقام الحاليّة بالمئات ولم تصل بعد لملايين الأرقام.
خصائص الأعداد الأوليّة
إذا كان (أ،ب) عددان صحيحان، وكان (ج) عدداً ثالثاً؛ حيث إنّ (ج) أوليّ، وكان حاصل ضرب العددين (أ × ب) يقبل القسمة على ج، فإنّ (أ) أو (ب) يقبلان القسمة على العدد (ج)، وهذا ما يُسمّى بمبرهنة إقليدس.
جميع الأعداد الأوليّة ما عدا (5،2) تنتهي بأحد الأعداد (9،7،3،1)؛ لأنّ الأعداد التي تنتهي بـ (8،6،4،2،0) هي من مضاعفات العدد اثنين فهي بذلك غير أوليّة، والأعداد التي تنتهي بـ (5،0) من مضاعفات العدد خمسة، وهي ليست أوليّة.
العدد 2 هو هو أصغر عدد في قائمة الأعداد الأوليّة، وهو العدد الزوجيّ الوحيد فيها.
تتوزع الأعداد الأوليّة بشكل غير منتظم، والسبب الرئيس يعود إلى عدم استيعاب العلماء لطريقة توزيع الأعداد الأوليّة، على النقيض من الأعداد الفردية والأعداد الزوجية، فكلما زادت قيمة العدد الأوليّ زادت الفجوة بينه وبين العدد الذي يليه.
أهميّة الأعداد الأوليّة
الأعداد الأولية، مثل إثنان، وثلاثة، وخمسة، وسبعة، تقبل القسمة على نفسها والرقم واحد فقط, وتلعب هذه الأعداد دوراً مهما في برمجة الكمبيوتر، وتعدّ الأعداد الأوليّة من أهمّ الأدوات التي تُستخدَم في تشفير البيانات الإلكترونيّة، والمعاملات البنكيّة، وتسجيل الدخول إلى مواقع التواصل الاجتماعيّ، والأعداد الأولية الكبرى مهمة في برمجة الحواسيب، كما تساعد في تأمين الخدمات البنكية الإلكترونية، والتسوق، والرسائل الخاصة.
الأعداد الأولية
– تعرف الأعداد الأولية في اللغة الإنجليزية باسم Prime numbers.
– يستخدم مصطلح العدد الأولي للتعبير عن العدد الطبيعيّ الذي لا يقبل القسمة إلّا على العدد واحد فقط وعلى نفسه فقط.
– إن العدد الأولي يمتلك قاسمين اثنين فقط، هما العدد واحد والرقم الأولي نفسه.
– بناءً على ما سبق فإن الأعداد التي تمتلك ثلاثة قواسم أو أكثر فإنه لا يمكن تصنيفها على أنها أعداد أولية.
– فيما يخص العدد واحد فإنه لا يعتبر عدداً أولياً ذلك أنه لا يمتلك إلّا قاسماً واحداً وهو نفسه، ونحتاج قاسمين اثنين حتى يصنف الرقم على أنه أولي وهذا الشرط يفتقر إلى العدد واحد.
– تعبر الأعداد الأولية عن مجموعة من الأعداد غير المنتهية، وقد استطاع العالم أقليدس أن يبرهن ذلك وكان ذلك في العام ثلاثمائة قبل الميلاد.
– الأعداد الأولية في طبيعتها لا تتبع صيغة محدّدة، وبالرغم من المحاولات لإيجاد ذلك إلا أن العلماء لم يستطيعوا ذلك.
-فيما يخص استعمال الأعداد الأولية فإنه يتم الاعتماد عليها في العديد من مجالات تكنولوجيا المعلومات.
– يتم استخدام الأعداد الأولية في مجال التشفير عن طريق المفتاح المعلن.
– بالإمكان معرفة الأعداد الأولية إذا كانت صغيرة وبسيطة ذهنياً، وذلك دون تعقيد.
– في حين أن الأعداد الصعبة والمعقدة لا يمكن الكشف عما إذا كانت أولية أو لا ببساطة أو بطرق ذهنية.
– تعتبر طريقة القسمة المتكررة هي أبرز الطرق وأكثرها شيوعاً واستخداماً للكشف عما إذا كان العدد أولي أو لا.
اكتشاف أكبر عدد أوليّ
لقد اكُشِف أكبر عدد أوليّ من قبل الدّكتور كيرتس كوبر في جامعة ميسوري في أمريكا عن طريق الحاسب الآليّ، ويتكوّن العدد الذي اكتُشِف من أكثر من 22 مليون رقماً، وهو أكبرمن العدد الأوليّ الذي اكتُشِفَ قبله بخمسة ملايين رقم تقريباً، والعدد الذي اكتُشِف حتى الآن حاصلٌ على الترتيب التاسع والأربعين في سلسلة أوليّة ميرسيني؛ وتفيد هذه الأرقام الأوليّة الكبيرة جداً في عمليّات الحوسبة للمستقبل؛ لأنّ الأرقام الحاليّة بالمئات ولم تصل بعد لملايين الأرقام.
خصائص الأعداد الأوليّة
تتميّز الأعداد الأوليّة بعدة خصائص، وهي:
-تتوزع الأعداد الأوليّة بشكل غير منتظم، والسبب الرئيس يعود إلى عدم استيعاب العلماء لطريقة توزيع الأعداد الأوليّة، على عكس الأعداد الفردية أو الأعداد الزوجية، فكلما زادت قيمة العدد الأوليّ زادت الفجوة بينه وبين العدد الذي يليه.
– جميع الأعداد الأوليّة ما عدا (5,2) تنتهي بأحد الأعداد (9,7,3,1)؛ لأنّ الأعداد التي تنتهي بـ (8,6,4,2,0) هي من مضاعفات العدد اثنين فهي بذلك غير أوليّة، والأعداد التي تنتهي بـ (5,0) من مضاعفات العدد خمسة، وهي ليست أوليّة.
– (إذا كان (أ،ب) عددان صحيحان، وكان (ج) عدداً ثالثاً؛ حيث إنّ (ج) أوليّ، وكان حاصل ضرب العددين (أ × ب) يقبل القسمة على ج، فإنّ (أ) أو (ب) يقبلان القسمة على العدد (ج)، وهذا ما يُسمّى بمبرهنة إقليدس.
– العدد 2 هو هو أصغر عدد في قائمة الأعداد الأوليّة، وهو العدد الزوجيّ الوحيد فيها.
أهميّة الأعداد الأوليّة
إنّ البيانات تستند في أمنها على مفاهيم عدّة، منها الأعداد الأوليّة؛ حيث تعدّ من أهمّ الأدوات التي تُستخدَم في تشفير البيانات الإلكترونيّة، والمعاملات البنكيّة، وتسجيل الدخول إلى مواقع التواصل الاجتماعيّ، ويكمن مبدأ عمل هذه الأعداد بتشفير المعلومات بشكل أوليّ، وتحويل الرسالة لرقم كبير ينتج عن ضرب عددين أوليّين كبيرين ببعضهما، حيث يُسمّى هذا الرّقم الفتاحَ؛ أي الرّقم السريّ، ولا يمكن اختراقه إلا إذا عُرِفت العوامل الأوليّة التي استُخدِمت لهذه العملية المُعقَّدة، وهذا من الصّعب جداً.