محصلة المتجهات في الفيزياء

محصلة المتجهات في الفيزياء وما المقصود بتحليل المتجه وأنواع المتجهات ومميزات المتجهات، هذا ما سوف نتعرف عليه فيما يلي.

محصلة المتجهات في الفيزياء

عند حركة جسم بين نقطتين او اكثر تتولد إزاحات متعددة لها قيمة واتجاه ولجل إيجاد المحصلة النهائية لإزاحة الجسم الكلية بين النقطة الأولى والنهائية تضاف هذه الإزاحات الى بعضها البعض او أن تطرح هذه الإزاحات من بعضها البعض (إذا كان اتجاهاتها متعاكسة) ولذلك يمكن تقسيم طريقة إيجاد محصلة الإزاحات إلى نوعين:

1- إضافة المتجهات (Vector Addition):
عند إضافة متجهين او اكثر إلى بعضها البعض يجب ان تكون هذه الكميات المتجهة من نفس النوع (إزاحات او قوى، مثلاً) وأن تكون ذلك وحدات قياس متماثلة.
2-طرح المتجهات (Subtraction of Vectors):
وتستخدم هذه الطريقة لإيجاد محصلة إزاحتان او اكثر عند تعاكس إحداها الاخرى في الاتجاه أو كلياً. ويمكن الاستفادة من مفهوم المتجه السالب (The Neghative of a Vector) لتغيير عملية طرح المتجهات إلى عملية جمع ثم التعامل معها. ويعرف المتجه السالب على أنه المتجه الذي إذا أضيف إلى المتجه الأصلي ستكون محصلة جمع المتجهين صفراً. فمثلاً إذا أضيف المتجه السالب (-A) إلى المتجه A كانت محصلة جمع المتجهين ستكون صفراً حيث المتجه –A يساوي بالقيمة المتجه A وبعاكسه بالاتجاه وكما يلي:
A+ (-A) = 0
واستناداً إلى هذا المفهوم يمكن تحويل عملية طرح أي متجهين إلى عملية جميع بأخذ المتجه السالب للثاني وكما يلي:
A-B = A+(-B)
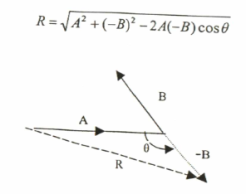
ويمثل الشكل التالي عملية طرح متجهين حيث يلاحظ أن المتجه B يعاكس جزئياً اتجاه حركة المتجه A، وهذا يحصل إذا زادت الزاوية المحصورة بين المتجهين المتعاقبين عن 90o، وبذلك يمكن رسم المتجه –B بالاتجاه المعاكس للمتجه B على ان يكون مساوياً له بالمقدار حيث عندئذ فقط يمكن معاملة المتجه A مع المتجه B- على أنها عملية جمع متجهين. ولإيجاد قيمة محصلة الحركة R، يجب معرفة الزاوية θ المحصورة بين المتجه A والمتجه –B ثم نستخدم قانون جيب التمام

ومن الميزات المهمة الاخرى للمتجهات أنها إذا ضربت بكمية غير متجهة (عديدة) فإن الناتج عبارة عن متجه جديد قيمته تساوي حاصل ضرب قيمة المتجه في قيمة الكمية العددية واتجاهه سوف يكون باتجاه الأولي، وكمثال على ذلك إذا ضرب المتجه A بالكمية غير المتجهة m فإن الناتج يساوي:
(mA = B = A×m) ، حيث B هو المتجه الجديد.

ما المقصود بتحليل المتجه

هو فرع من الرياضيات يتعامل مع الكميات ذات الحجم والاتجاه، ويمكن تحديد بعض الكميات الفيزيائية والهندسية، المسماة بالكميات، بشكل كامل من خلال تحديد حجمها في وحدات قياس مناسبة، وهكذا يمكن التعبير عن الكتلة بالجرام، ودرجة الحرارة بالدرجات على مقياس ما، والوقت بالثواني. يمكن تمثيل المقاييس بيانياً بنقاط على بعض المقاييس الرقمية مثل الساعة أو مقياس الحرارة، وهناك أيضًا كميات، تسمى المتجهات تتطلب تحديد الاتجاه بالإضافة إلى الحجم، تعد السرعة والقوة والإزاحة أمثلة على المتجهات، ويمكن تمثيل كمية المتجه بيانياً بواسطة مقطع خط موجه، ويُرمز إليه بسهم يشير في اتجاه كمية المتجه، ويمثل طول المقطع حجم المتجه.

أنواع المتجهات

1-المتجهات الأولية المشتركة
تسمى المتجهات التي لها نفس نقطة البداية متجهات أولية مشتركة.
2-المتجه الصفري
المتجه الصفري هو متجه عندما يكون حجم المتجه صفراً وتتزامن نقطة بداية المتجه مع النقطة النهائية ، ويترتب على ذلك أن حجم المتجه الصفري يساوي صفرًا وأن اتجاه هذا المتجه غير محدد.
3-المتجهات الخطية
المتجهات التي تقع على نفس الخط أو الخطوط المتوازية معروفة بأنها متجهات خطية ، تُعرف أيضًا باسم المتجهات المتوازية.
4-المتجهات المشتركة المستوية
تُعرف ثلاثة نواقل أو أكثر تقع في نفس المستوى أو موازية لنفس المستوى باسم المتجهات المشتركة المستوية.
5-المتجهات المتشابهة
تُعرف المتجهات التي لها نفس الاتجاه باسم المتجهات المتشابهة ، على العكس من ذلك ، يُطلق على المتجهات التي لها الاتجاه المعاكس فيما يتعلق ببعضها البعض أنها غير متشابهة

مميزات المتجهات

– هناك الكثير من المميزات التي تميز بها المتجهات و تجعل منها هامة للغاية ، حيث أن المتجهات توفر لنا إمكانية قياس و معرفة الجهات الموجودة في أي مبنى أو عقار مختلف ، كما أن المتجهات تساعد على معرفة الفروق الموجودة بين الكميات المتجهة و بين الكميات السليمة و تمنحنا القدرة على التمييز بين هذه الكميات المختلفة .
-كما أنه من خلال المتجهات يمكننا تصنيف الكميات الفيزيائية المختلفة إلى كميات عددية و كميات متجهة ، من الممكن تمثيل المتجهات المختلفة من خلال الرسم ، يتم تحليل المتجهات من خلال عدة مستويات تضم محورين يقعان متعامدين و من خلالهما نحصل على قيمة كل متجه و نتعرف من خلالها على المركبات الصادية و السينية و العينية