مساحة المستطيل بمعلومية طول قطره

مساحة المستطيل بمعلومية طول قطره وماهو المستطيل وحساب مساحة المربع وخصائص المربع، هذا ما سوف نتعرف عليه فيما يلي.

مساحة المستطيل بمعلومية طول قطره

-الطريقة الاولى .
لحساب مساحة المستطيل هناك معادلة اساسية من خلالها يتم حساب مساحتة و هى : –
مساحة المستطيل = الطول ( ل ) X العرض ( ع ) و الناتج يحسب بالسم المربع او المتربع او ايًا كانت ودة القياس المستخدمة المهم ان وحدة قياس المساحة هى التربيع .
مثال : – مستطيل طوله يساوي 10 سم و عرضه يساوي 7 سم اوجد مساحة المستطيل .
الحل .
مساحة المستطيل = ل X ع = 10 X 7 = 70 سم2
و من خلال هذا القانون تستطيع الحصول على الطول او العرض بقوانين متفرعة منه و لكن هنا يجب ان يكون بالمعادلة مجهول واحد اي انه للحصول على طول المستطيل يكون معطى لنا العرض و المساحة او العكس .
الطول ( ل ) = المساحة \العرض ( ع )
العرض ( ع ) = المساحة \ الطول ( ل )
مثال : – مستطيل مساحته 72سم2 و طوله يساوي 12 سم او جد عرضة .
الحل .
ع = المساحة \ الطول = 72\12 = 6 سم
مثال : – مستطيل مساحته 36 سم2 و عرضه يساوي 4 سم احسب طوله .
الحل .
ل = 36\4 = 9 سم
-الطريقة الثانية
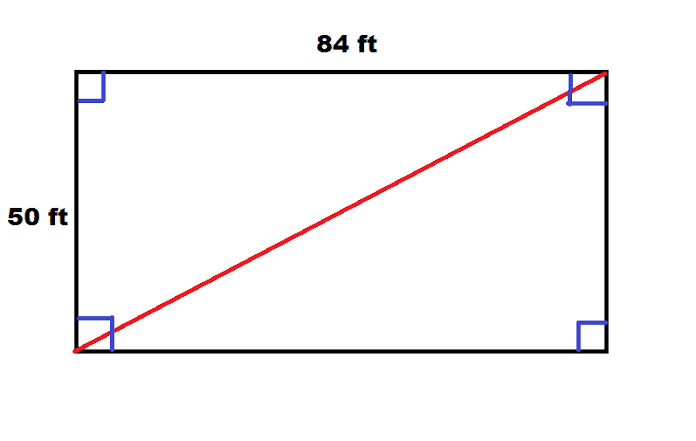
تطبيق نظرية فيثاغورث عندما يكون معلوم لديك طول احد اجناب المستطيل و قطره هنا تستطيع تطبيق نظرية فيثاغورث للحصول على الحد الثاني , من المعروف انه من خواص المستطيل ان كل زواياه الاربع قوائم اي ان كل زاوية يحدها ضلعين من اضلاع المستطيل احدهما يكون الطول و الآخر العرض هما ضلعي الزاوية القائمة او ما نطلق عليه ضلعي القائمة و القطر هنا يمثل الوتر او الضلع المقابل للزاوية القائمة , لذا فانه يمكن تطبيق نظرية فيثاغورث الخاصة بالمثلث القائم الزاوية و تساعدنا في الحصول على ايًا من ضلعي القائمة او حرفي المستطيل بمعلومية الضلع الثاني و الوتر .
معادلة نظرية فيثاغورث .
مربع طول الوتر = مجموع مربعي ضلعي القائمة .
في حال المستطيل .
مربع القطر = مرع الطول + مربع العرض .
القوانين الفرعية .
الطول = الجذر التربيعي لمربع القطر – مربع العرض .
العرض = الجذر التربيعي لمربع القطر – مربع الطول .
مثال : – مستطيل طول قره 10 سم و عرضه يساوي 6 سم احسب مساحة المستطيل .
الحل .
طول المستطيل = الجذر التربيعي لمربع القطر – مربع العرض
= الجذر التربيعي لـ 100 – 36
= الجذر التربيعي لـ 64 = 8 سم .
مساحة المستطيل = الطول X العرض = 6 X 8 = 48سم2
مثال : – مستطيل طول قطره 5 سم و طوله يساوي 4 سم اوجد مساحته .
الحل .
عرض المستطيل = الجذر التربيعي لمربع القطر- مربع الطول .
= الجذر التربيعي لـ 25 – 16
= الجذر التربيعي لـ 9 = 3سم .
مساحة المستطيل = الطول X العرض = 3 X 4 = 12 سم2 .

ما هو المستطيل

المستطيل (بالإنجليزية: Rectangle)، هو شكل من الأشكال الهندسية، ويحتوي المستطيل على أربعة أضلاع، بحيث يكون كل ضلعين متقابلين متساويين بالطول، وإن الإختلاف الوحيد بين المستطيل والمربع هو أن المربع جميع أطوال أضلاعه متساوية، وفي الواقع يحتوي المستطيل على أربعة زوايا قائمة، بحيث تكون كل زاوية من الزاويا الأربعة بمقدار 90 درجة، ومجموع زواياه يكون 360 درجة، ويمكن القول أن المستطيل هو نوع خاص من متوزاي الأضلاع، وإن المربع هو نوع خاص من المستطيل، وبسبب إن المستطيل لا يحتوي على أي إرتفاع لذا يعتبر من الأشكال ثنائية الأبعاد، حيث يكون له طول وعرض فقط.

حساب مساحة المربع

المربع هو عبارة عن شكل رباعي متساوي الأضلاع وجميع زواياه متساوية وتعادل 90 درجة، ومن أجل معرفة أن الشكل الذي أمامك مربع لابد من توافر أربعة أشياء يجب أن يتصف بهم المربع وهم كالآتي:
-لابد من أن يكون الشكل الذي أمامك متساوي السطح من أجل أن يكون مربع. يجب أن يكون الشكل رباعي الأضلاع وأضلاعه متساوية في الطول.
-لابد أن يكون المضلع منتظم في الشكل.
– يجب أن يكون الشكل الذي أمامك مغلق. والطريقة الأولى لحساب مساحة المربع وهي طول الضلع في نفسه والي يطلق عليها طول الضلع × طول الضلع، فإذا افترضنا أن يرمز لمساحة المربع بالرمز س ويرمز لطول الضلع بالرمز م فبالتي س= م×م، فعلى سبيل المثال:
– مربع طول ضلعه يساوي 4 فما هي مساحة المربع؟ س= م×م، مساحة المربع= 4×4= 16 م2. مربع طول ضلعه يساوي 6 متر، فما هي مساحة المربع؟ س=م×م، ومساحة المربع= 6×6= 36 م2.

خصائص المربع

المربع هو شكل منتظم من الأشكال الهندسية، له عدد من الخصائص التي تميزه منها ما يلي:
-جميع أضلاع المربع متساوية في الطول، لذلك فإن المربع هو مضلعًا. كل ضلعين متقابلين في المربع متوازيان، أي لا تتقاطع الأضلاع المتقابلة أبدًا.
– المربع من الأشكال المسطحة وبالتالي فإنه ثنائي الأبعاد. المربع له قطران ذات طول متساوي، ومتعامدان إذ يشكل التقائها زوايا 90 درجة، كما ينصف كل منهما الآخر.
-كل زوايا المربع زوايا قائمة، لها نفس القياس، حيث إن قياس كل زاوية يساوي 90 درجة، وبالتالي فإن أضلاع المربع متعامدة.
-مجموع الزوايا الداخلية للمربع متساوية مجموعها يساوي 360 درجة. المربع له أربعة محاور تماثل، اثنان من تلك المحاور يمثلان قطر المربع، والاثنان الآخران هما منصفان الجوانب المتقابلة.
– المستطيل يصبح مربعًا، إذا كانت جميع أضلاع المستطيل متساوية ومتطابقة. المعين يسمى مربعًا، إذا كانت كل زاوية من زوايا المعين قائمة أي قياسها 90 درجة.