مساحة المستطيل للصف الخامس

مساحة المستطيل للصف الخامس مساحة المثلث للصف الخامس اوجد مساحة المستطيل المجاور كيف تحسب مساحة المستطيل تجدون كل تلك الموضوعات من خلال مقالنا هذا

مساحة المستطيل للصف الخامس

1-المستطيل هو شكل ثنائي الأبعاد، وهو رباعي أضلاع حيث تكون زواياه الأربعة قائمة. ينبع من هذا أنّ للمستطيل زوجين من الضلعين المتقابلين والمتساويين؛
2-المساجة= الطول × العرض
3-المحيط = (الطول + العرض ) × 2

مساحة المثلث للصف الخامس

1-محيط المثلث (أو) محيط اي مضلع = مجموع اطوال اضلاعه ، بينما محيط المثلث المتساوي الاضلاع = طول الضلع × 3
2-طول ضلع المثلث المتساوي الاضلاع = محيط المثلث ÷ 3
3-مساحة المثلث = نصف × طول القاعدة × الارتفاع .
4-طول قاعدة المثلث = 2 × مساحة المثلث ÷ الارتقاع
5-ارتفاع المثلث = 2 × مساحة المثلث ÷ طول القاعدة
6-مثلث طول قاعدته 6 سم وارتفاعه 3سم فإن مساحته = …. سم مربع
7-مساحة المثلث = نصف × طول القاعدة × الارتفاع = نصف × 6 × 3 = 3 × 3 = 9 سم مربع
8-مثلث مساحته 24 سم مربع ، طول قاعدته 6سم ، فإن ارتفاعه = …. سم
9-ارتفاع المثلث = 2 × مساحة المثلث ÷ طول القاعدة = 2 × 24 = 48 ÷ 6 = 8 سم
10-مثلث مساحته 40 سم مربع ، وإرتفاعه 8سم ، فإن طول قاعدته = ….. سم
11-طول قاعدة المثلث = 2 × مساحة المثلث ÷ الارتفاع = 2 × 40 ÷ 8 = 80 ÷ 8 = 10 سم

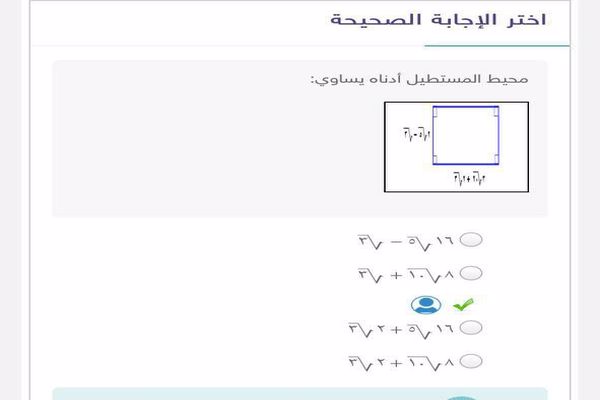
اوجد مساحة المستطيل المجاور

1-المستطيل عبارة عن شكل هندسي يشبه المربع في كثير من الخصائص، فكلاهما يمتلك اربع اضلاع واربع زوايا قائمة ولكن المستطيل يختلف عن المربع في طول الاضلاع حيث ان جميع اضلاع المربع متساوية اما المستطيل فكل ضلعين متقابلين متساويين، وفيما يخص سؤالنا هذا
2-ما مساحة المستطيل المجاور
3-الاجابة هي: مساحة المستطيل= طول الضلع الأول (الطول) × طول الضلع الثاني (العرض).
4-مساحة المستطيل المجاور = 147 وحدة مربعة.

كيف تحسب مساحة المستطيل

الطريقة الاولي
1- لحساب مساحة المستطيل هناك معادلة اساسية من خلالها يتم حساب مساحتة و هى : –
مساحة المستطيل = الطول ( ل ) X العرض ( ع ) و الناتج يحسب بالسم المربع او المتربع او ايًا كانت ودة القياس المستخدمة المهم ان وحدة قياس المساحة هى التربيع .
2-مثال : – مستطيل طوله يساوي 10 سم و عرضه يساوي 7 سم اوجد مساحة المستطيل .
الحل .
مساحة المستطيل = ل X ع = 10 X 7 = 70 سم2
و من خلال هذا القانون تستطيع الحصول على الطول او العرض بقوانين متفرعة منه و لكن هنا يجب ان يكون بالمعادلة مجهول واحد اي انه للحصول على طول المستطيل يكون معطى لنا العرض و المساحة او العكس .
الطول ( ل ) = المساحة \العرض ( ع )
العرض ( ع ) = المساحة \ الطول ( ل )
3-مثال : – مستطيل مساحته 72سم2 و طوله يساوي 12 سم او جد عرضة .
الحل .
ع = المساحة \ الطول = 72\12 = 6 سم
4-مثال : – مستطيل مساحته 36 سم2 و عرضه يساوي 4 سم احسب طوله .
الحل .
ل = 36\4 = 9 سم
الطريقة الثانية
1-تطبيق نظرية فيثاغورث عندما يكون معلوم لديك طول احد اجناب المستطيل و قطره هنا تستطيع تطبيق نظرية فيثاغورث للحصول على الحد الثاني , من المعروف انه من خواص المستطيل ان كل زواياه الاربع قوائم اي ان كل زاوية يحدها ضلعين من اضلاع المستطيل احدهما يكون الطول و الآخر العرض هما ضلعي الزاوية القائمة او ما نطلق عليه ضلعي القائمة و القطر هنا يمثل الوتر او الضلع المقابل للزاوية القائمة , لذا فانه يمكن تطبيق نظرية فيثاغورث الخاصة بالمثلث القائم الزاوية و تساعدنا في الحصول على ايًا من ضلعي القائمة او حرفي المستطيل بمعلومية الضلع الثاني و الوتر .
معادلة نظرية فيثاغورث .
مربع طول الوتر = مجموع مربعي ضلعي القائمة .
في حال المستطيل .
مربع القطر = مرع الطول + مربع العرض .
القوانين الفرعية .
الطول = الجذر التربيعي لمربع القطر – مربع العرض .
العرض = الجذر التربيعي لمربع القطر – مربع الطول .
2-مثال : – مستطيل طول قره 10 سم و عرضه يساوي 6 سم احسب مساحة المستطيل .
الحل .
طول المستطيل = الجذر التربيعي لمربع القطر – مربع العرض
= الجذر التربيعي لـ 100 – 36
= الجذر التربيعي لـ 64 = 8 سم .
مساحة المستطيل = الطول X العرض = 6 X 8 = 48سم2
3-مثال : – مستطيل طول قطره 5 سم و طوله يساوي 4 سم اوجد مساحته .
الحل .
عرض المستطيل = الجذر التربيعي لمربع القطر- مربع الطول .
= الجذر التربيعي لـ 25 – 16
= الجذر التربيعي لـ 9 = 3سم .
مساحة المستطيل = الطول X العرض = 3 X 4 = 12 سم2 .