مساحة المستطيل للصف السادس، ومساحة المستطيل والمربع، وتعريف المستطيل، وخصائص المستطيل، وخواص المستطيل، وقوانين المستطيل، وأمثلة على مساحة المستطيل، وما هي مادة الرياضيات؟، وكيف أذاكر الرياضيات وأحصل على أعلى الدرجات؟، نتناول الحديث عنهم بشيء من التفصيل خلال المقال التالي.
محتويات المقال
مساحة المستطيل للصف السادس

يكون قانون مساحة المستطيل للصف السدس كما يلي:
– مساحة المستطيل = الطول × العرض.
مساحة المستطيل والمربع
يتمثل قانون مساحة المستطيل والمربع فيما يلي:
1. مساحة المستطيل = الطول × العرض.
2. مساحة المربع = طول ضلع نفسه.
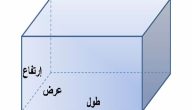
المساحة الكلية للمكعب للصف السادس
يكون قانون المساحة الكلية للمكعب للصف السادس كما يلي:
1. المساحة الجانبية للمكعب = 4 × طول الحافة المربعة.
2. المساحة الإجمالية للمكعب = 6 × طول حافة المربع.
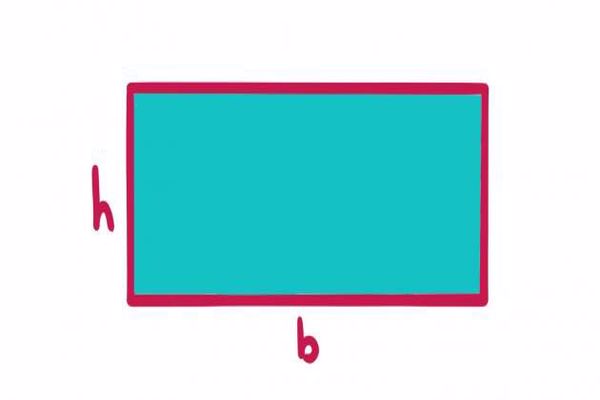
تعريف المستطيل
في الهندسة الأقليدية، المستطيل هو شكل ثنائي الأبعاد، وهو رباعي أضلاع حيث تكون زواياه الأربعة قائمة، ينبع من هذا أنّ للمستطيل زوجين من الضلعين المتقابلين والمتساويين؛ أي أنّ المستطيل هو حالة خاصة من متوازي أضلاع تكون كل زواياه قائمة. كما يعتبر المربع حالة خاصة من المستطيل تكون فيها أطوال الأضلاع الأربعة متساوية.
خصائص المستطيل
1. قُطرا المُستطيل متساويا الطّول.
2. قُطرا المستطيل يُنصّف كلّ منهما الآخر.
3. كلُّ ضلعَين متقابِلَين في المُستطيل متوازيان.
4. كلُّ ضلعَين مُتقابلَينِ في المُستطيل متساويا الطّول.
6. المُستطيل هو أحد أشكال متوازي الأضلاع، إلّا أنَّ زواياه قائمة.
خواص المستطيل
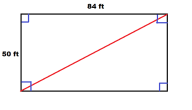
عمومًا ما يطلق على الضلع الأطول في المستطيل أسم الطول، وعلى الضلع الأقصر أسم العرض. وتكون مساحة المستطيل حاصل ضرب طوله وعرضه، حيث إن في المستطيل تكون جميع الزوايا قائمة، وكل ضلعين متقابلين متوازيين ومتساويين. لأنّه نوع خاص من متوازي أضلاع، فإنّ أقطار المستطيل متساوية الطول وتنصّف بعضها البعض. بعكس المربع والمعين فإنّ أقطار المستطيل غير متعامدة ولا تنصف زواياه، لأنّ زوايا المستطيل قائمة، بالإمكان إيجاد طول قطره، c، من عرضه، a، وطوله، b، بواسطة قانون فيثاغورس.
– قد يستخدم المستطيل أيضًا في حساب تكامل ريمان التقريبي لتكامل دالّة، بواسطة تحويل المساحة الموجودة تحت الرسم البياني للدالة إلى سلسلة من المستطيلات ذات عرض صغير، وطول يساوي معدّل قيمة الدالة في الجوار.
قوانين المستطيل
بما أنّ المستطيل شكل ثنائي البعد يمتاز بأنّ له بعدين هما العرض والطول، إذن يمكن حساب محيطه من المعلومات المعروفة لدى الجميع عن المضلعات المنتظمة الرباعية، وبالتالي فإنّ محيطه هو عبارة عن مجموع أطوال أضلاعه، وبصيغة رياضية يُكتب قانون محيطه كما يلي:
1. محيط المستطيل=مجموع أطوال أضلاعه
2. محيط المستطيل=2×(الطول +العرض)
أما عن قانون مساحته فإنّها تساوي حاصل ضرب طوله في عرضه، وبصيغة رياضية تُمَثَّل كما يلي:
1. مساحة المستطيل=الطول ×العرض.
أمثلة على مساحة المستطيل
1. المثال الأول
لنفترض أنه لدينا مستطيل صغير، طوله 8 سم، وعرضه 4 سم، كم تبلغ مساحة المستطيل؟
لحساب مساحة المستطيل، نضرب الطول في العرض أي: 8*4= 32 سم2.
2. المثال الثاني
نريد بناء فناء صغير بطول 12م وعرض 10م، وننوي استخدام أحجار لرصفه، كم مترًا مربعًا من الأحجار نحتاج لشرائها لرصف كامل المساحة؟
لحساب مساحة الفناء، والتي حسب نص المسألة، تعتبر مساحة المستطيل المشكّل للفناء، نقوم بعملية ضرب طول الفناء بعرضه أي 10*12= 120 مترًا مربعًا من الأحجار لرصف الفناء كله.
3. المثال الثالث
تصطف الوحدات في ثلاثة صفوفٍ من خمسة مربعاتٍ، كيف يمكن إذن إيجاد العدد الكلي للوحدات؟
بعملية ضرب 3 * 5= 15، أو يمكن أن نقول: يحتوي المستطيل على خمسة أعمدةٍ من ثلاثة مربعاتٍ، وعلى ذلك نحصل على مساحة المستطيل الإجمالية أيضًا وهي 5* 3=15.5.
ما هي مادة الرياضيات؟
– مادة الرياضيات اكتشفت منذ قديم الزمان أي منذ نشأة الإنسان، لذلك ليس لها تعريف موحد لأن كل عصر يقوم بالتطوير من علوم الرياضيات وإضافة أشياء جديدة على التعريف، فأرسطو كان يطلق عليه علم الكميات، حيث يقصد به قدرة الإنسان على عد الأشياء، ومعرفة كمياتها، وهذا أمر بديهي لدى الإنسان أي يوجد في فطرته مع تعلم بسيط، ثم تطورت الرياضيات في عصر السامرين والبابليين والفراعنة، حيث أثبتت الدراسات أنهم كانوا يستخدمون علم القياس والجبر وعلم الفلك والعلوم المالية والبناء، أي يستخدمون الرياضيات في أغلب الجوانب الحياتية.
– انتشرت العلوم الرياضية وأخذت ذروتها في العصور الإسلامية، علم الرياضيات من العلوم التي ترتبط ارتباط وثيق بعلوم أخرى مثل علم الفيزياء والكيمياء وعلم الأحياء البيولوجيا.
– من فروع الرياضيات؛ التفاضل والتكامل والهندسة الرياضية ونظرية الأعداد والجبر ومعادلات تفاضلية وطوبولوجيا، فالرياضيات يستخدمونها لإثبات الحقيقة عن طريق تخمين دقيق للأشياء والتعاريف المختارة بشكل مناسب.
– عرف الرياضي الفرنسي أوزانا سنة 1691، الرياضيات هي العلم الذي يدرس كل ما يمكن قياسه أو حسابه، وتم تدريس الرياضيات في كافة المراحل التعليمية سواء في المدرسة الابتدائية أو الإعدادية والثانوية، كذلك الجامعات ولها تخصصات عامة بها في الكلية، وذلك لاهتمامها وارتباطها الوثيق بحياتنا اليومية.
كيف أذاكر الرياضيات وأحصل على أعلى الدرجات؟
1 – حاول تحضير الدروس قبل تلقيها من المعلم
دراسة وتحضير الدروس قبل تلقيها من المعلم أمر أساسي مع كل المواد، ولكن مع الرياضيات مهم للغاية على الرغم من أن معظم الطلاب يعتقدون أنه من الصعب تحضير دروسها، ولكن ليس عليك إتقان الدرس، إنها مجرد محاولات لفهم أكبر قدر ممكن من المعلومات.
2 – الانتباه خلال شرح الدروس والتركيز مع المعلم
لنتخيل أنك شعرت بالملل خلال محاضرة الرياضيات، وتوقفت عن التركيز مع المعلم، ومن ثم لم تذاكر هذه المعلومات وبقيت هكذا إلى فترة الامتحانات، عندها ستكتشف وجودها للمرة الأولى ستتفاجأ من أين أتى هذا الرقم؟ وما هذه المعادلة؟ وكيف حصلنا على هذا الناتج؟
3 – اطرح الأسئلة في حال وجود أي أفكار غير مفهومة
الرياضيات من المواد التراكمية المترابطة بشكل وثيق، فدرس اليوم يعتمد بشكل كبير جدًا على درس اليوم السابقة بالإضافة إلى دروس الأعوام السابقة، وبالتالي احتمال وجود أفكار وفقرات غير مفهومة احتمال وارد قد تنتج في كثير من الأحيان عن نسيان المعلومات السابقة.
4 – دراسة الأفكار في نفس يوم تلقي الدرس
حتى الآن أنت قد ذاكرت الرياضيات مرتين: الأولى في تحضير الدروس والثانية خلال التركيز مع الدرس بالإضافة إلى فهم كل الفقرات والأسئلة التي قمت بطرحها، وهذه المعلومات ما تزال كاملة طازجة في دماغك.
5 – حل المسائل والتمارين بنفسك
الإمساك بالكتاب أو الدفتر وتصفحه أو قراءة الملخص الذي قمت بصنعه قد يمكنك من إنهاء الدراسة بسرعة ولكن في الامتحان سوف تظهر مفاجآت لم تكن تتوقع وجودها وسوف تواجه صعوبات ظننت أنها سهلة، حيث إن أساس كيف أذاكر الرياضيات هو الحل بنفسك بيدك أنت وبالكثير من التركيز، وما عليك إلا وضع الملخص بالقرب منك وحل كل التمارين والمسائل الموجودة في الكتاب بالإضافة إلى التمارين التي قام المعلم بحلها.