مساحة المستطيل والمربع

مساحة المستطيل والمربع وشرح محيط المستطيل وحساب حجم المكعّب وتعريف المحيط والمنطقة، هذا ما سوف نتعرف عليه فيما يلي.

مساحة المستطيل والمربع

-المستطيل :
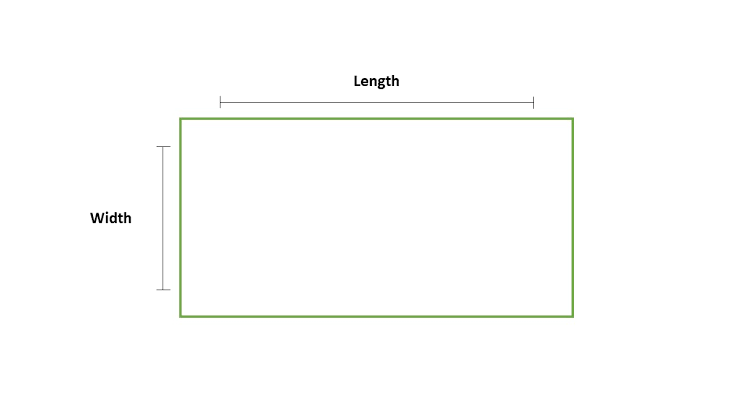
المستطيل هو شكل ثنائي الأبعاد، وهو رباعي أضلاع حيث تكون زواياه الأربعة قائمة. ينبع من هذا أنّ للمستطيل زوجين من الضلعين المتقابلين والمتساويين؛
المساحة = الطول × العرض
المحيط = (الطول + العرض ) × 2
المربع:
المربع هو مضلع منتظم يتكون من أربعة أضلاع متساوية في الطول ومتعامدة تشكل أربع زوايا قائمة
المساحة = طول الضلع × نفسه
المحيط = طول الضلع × 4

شرح محيط المستطيل

1-اكتب المعادلة الأساسية لإيجاد محيط المستطيل.

ستساعد هذه المعادلة في إرشادك عند حساب محيط المستطيل. المعادلة الأساسية هي: المحيط = 2 (الطول + العرض).
المحيط دومًا هو المسافة الكلية بامتداد الحواف الخارجية لأي شكل، سواءً كان بسيطًا أم مركبًا.
سنرمز للمحيط في هذه المعادلة ب رمز “م” و”ط” لطول المستطيل و”ع” لعرضه.
قيمة الطول أكبر من العرض دومًا.
سيتساوى الطولان والعرضان في المستطيل نظرًا لتساوي الأضلاع المتقابلة. هذا سبب كتابتنا للمعادلة كعملية ضرب لمجموع الطول والعرض في 2.
كما يمكنك كتابة المعادلة م = ط + ط + ع + ع لتوضيح هذه المسألة أكثر.
2-جد طول المستطيل وعرضه.

ستعطى طول المستطيل وعرضه في المسألة بالنسبة لمسائل الرياضيات البسيطة؛ عادة ما توضح هذه القيم بجوار رسم المستطيل.
استخدم مسطرة أو عصا أو شريط قياس لإيجاد طول وعرض المساحة التي تحاول حسابها إذا كنت تحسب محيط مستطيل في الواقع. قس كل الأضلاع إذا كنت خارج البيت لترى ما إذا كانت الأضلاع المتقابلة تتطابق حقًا.
مثال: الطول = 14 سم والعرض = 8 سم.
3-اجمع الطول والعرض.

عليك أن تعوض بقيم الطول والعرض في المعادلة بعد تحديدها.
لاحظ عند حل معادلات المحيط أن العمليات الموجودة داخل الأقواس المربعة أو العادية تحل قبل الموجودة خارجها وفقًا لأولوية العمليات. لهذا ستبدأ بحل المعادلة بجمع الطول والعرض.
على سبيل المثال: المحيط = 2* (الطول + العرض) = 2 (14 + 8) = 2*22.
4-اضرب مجموع الطول والعرض في 2. يضرب (الطول + العرض) في 2 عند النظر لمعادلة إيجاد محيط المستطيل وستحصل على المحيط حين تتم عملية الضرب هذه.
تأخذ عملية الضرب هذه في الحسبان ضلعي المستطيل الآخرين. لقد جمعت ضلعين فقط من الشكل عند جمع الطول والعرض.
يمكنك ضرب الناتج في 2 لإيجاد مجموع كل الأضلاع نظرًا لتساوي جانبي المستطيل الآخرين مع الجانبين المجموعين.
على سبيل المثال: المحيط = 2 * (الطول + العرض) = 2 *(14+8) = 2*22 = 44 سم.
5-اجمع “الطول + الطول + العرض + العرض”.

يمكنك جمع الأضلاع الأربعة معًا مباشرة لإيجاد محيط المستطيل بدلًا من جمع ضلعين وضرب الناتج في 2.

هذه نقطة بداية رائعة إذا كنت تجد صعوبة في مفهوم المحيط.
على سبيل المثال: المحيط = الطول +الطول +العرض + العرض = 14 + 14 + 8 + 8 = 44 سم.

حساب حجم المكعّب

يُحسَب حجم المكعّب مهما كان حجمه صغيراً أو كبيراً، بالاعتماد على القانون الآتي:
-قانون حجم المكعّب= الطّول×العرض×الارتفاع
ونظراً لأنّ الطول= العرض= الارتفاع؛ فإنّ:
حجم المكعّب= طول الحرف(الضّلع)×طول الحرف(الضّلع)×طول الحرف(الضّلع)= القوّة الثالثة للعدد، ويرمز له: س³.
-حساب مساحة المكعّب المساحة الكليّة
تُحسَب المساحة الكليّة للمكعّب كما يأتي:
المساحة الكليّة للمكعّب= 6×(مربّع طول الحرف (الضّلع))
-المساحة الجانبيّة
تُحسَب المساحة الجانبيّة للمكعّب كما يأتي:
المساحة الجانبيّة للمكعّب= 4×(مربّع طول الضّلع)

تعريف المحيط والمنطقة

-تعريف المحيط
يتم تعريف المحيط كمقياس لطول الحد الذي يحيط بالشكل الهندسي المغلق. مصطلح “محيط” مشتق من الكلمة اليونانية “بيري” و “متر” والتي تعني حولها وقياسها. في الهندسة ، فإنه يشير إلى الخط المستمر الذي يشكل المسار خارج الشكل ثنائي الأبعاد.
بكلمات بسيطة ، المحيط ليس سوى طول الخطوط العريضة للشخصية. لمعرفة محيط كائن معين ، يمكنك ببساطة إضافة طول الجوانب للوصول إلى محيطه. يُعرف محيط الدائرة عادة باسم محيطها.
على سبيل المثال : لنفترض أنك قمت بلف سلسلة حول المربع ، وطول السلسلة سيكون محيطها.
ب. أنت تتجول خارج الحديقة ، ستكون المسافة المغطاة محيط الحديقة.
-تعريف المنطقة
في الرياضيات ، يتم تعريف مساحة سطح مستو على أنها مقدار المساحة التي تغطيها. وهي كمية مادية تشير إلى عدد الوحدات المربعة التي يشغلها الكائن ثنائي الأبعاد. يتم استخدامه لمعرفة مقدار المساحة التي يشغلها سطح مستو. يتم قياسها بوحدات مربعة ، أي متر مربع ، ميل مربع ، بوصة مربعة ، إلخ.
مصطلح المدى له عدد من الاستخدامات العملية مثل في مشاريع البناء ، الزراعة ، الهندسة المعمارية ، وهلم جرا. لقياس مساحة سطح مستو ، تحتاج إلى حساب عدد المربعات التي يغطيها الشكل.