تعريف المصفوفات وانواعها نتحدث عنها بشكل من التفصيل من خلال مقالنا هذا كما نذكر لكم تعريف المصفوفات في الحاسب هذا بالإضافة إلى مقدمة في المصفوفات وختام الموضوع تعاريف خاصة بالمصفوفات تابعوا السطور القادمة.
محتويات المقال
تعريف المصفوفات وانواعها
تعريف المصفوفات
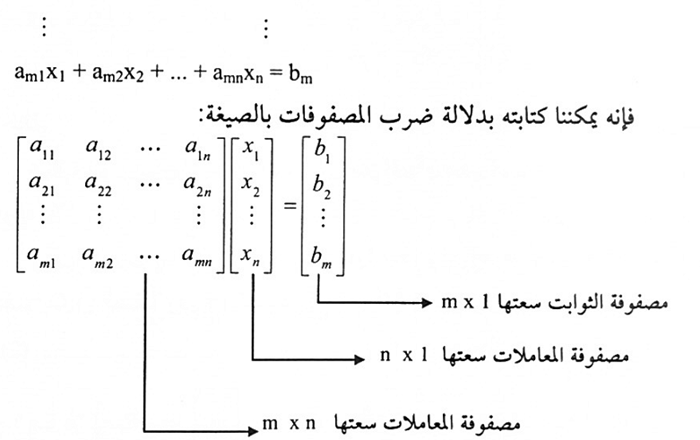
هي مجموعةٌ من الأرقام مرتبةٌ في عددٍ من الصفوف والأعمدة، عادةً تكون هذه الأرقام حقيقيةً ويمكن أن تكون معقدةً كما يمكن تعريفها بشكلٍ عام بأنها دالة رياضية خطيّة تحول مجموعة بداية أي منطلقٍ، إلى مجموعة وصول أو نهاية (مستقر) ومجموعة المنطلق والمستقر يمكن أن تكون مكونةً من أعدادٍ صحيحةٍ أو عقدية أو أشعة من الأعداد، كما يمكن أن تكون هاتان المجموعتان مكونتان من دالاتٍ رياضيةٍ أو أشعة دالات رياضية، ونرمز للمصفوفة بقوسين مربعين كبيرين أو هلالين يُكتب ضمنها عناصر المصفوفة
أنواع المصفوفات
توجد أنواع مختلفة للمصفوفات التي تستخدم في الحل ومنها:
1-مصفوفة الصف
تتكون مصفوفة الصف من صف واحد فقط وليس مشروط عدد الأعمدة فيمكن أن تحتوي على عدد كبير من الأعمدة فيمكن أن تكون من رتبة 1 x 5 على سبيل المثال فيتم البداية بعدد الصفوف ثم عدد الأعمدة.
2-مصفوفة العمود
تعتبر مصفوفة العمود هي مصفوفة تحتوي على عمود واحد فقط من الأرقام مع عدد غير محدود من الصفوف فعلى سبيل المثال المصفوفة من الرتبة 5 x 1 فالعدد 5 يعبر عن عدد الصفوف والعدد 1 يدل على العمود الواحد.
3-المصفوفة المربعة
في المصفوفة المربعة يكون عدد الأعمدة مساوي تماما لعدد الصفوف حيث تكون الرتبة متساوية فيجب أن يساوي n=m ويمكن أن يقال إنها من الرتبة m.
4-المصفوفة المستطيلة
تعتبر المصفوفة المستطيلة هي المصفوفة التي يكون بها عدد الصفوف لا يساوي عدد الأعمدة وتكون الرتبة بهذا الشكل: 2 x 3 أو 4 x 2 وهكذا.
5-المصفوفة العددية
تعتبر المصفوفة العددية هي مصفوفة قطرية ولكن يجب أن يحتوي القطر على عدد ثابت لا يتغير غير الصفر ويقال عن المصفوفة القطرية أنها مصفوفة عددية في حالة إذا كان القطر عناصره متساوية مثل المصفوفة المربعة.
6-مصفوفة الوحدة
تعتبر مصفوفة الوحدة هي المصفوفة المربعة التي تحتوي جميع عناصرها على أصفار ما عدا القطر يحتوي على الرقم واحد وتسمى أيضا بمصفوفة الهوية.
8-المصفوفة القطرية
تحتوي المصفوفة القطرية على أرقام في القطر فقط وباقي المصفوفة مكونة من أصفار ويتم التعبير عنها بالرتبة m x n مثل باقي المصفوفات.
9-مصفوفة الصفر
تعتبر مصفوفة الصفر هي المصفوفة التي تحتوي على أصفار في جميع العناصر مثل المصفوفة: [000000000]
10-المصفوفة المعكوسة
تعتبر المصفوفة المعكوسة هي المعكوس للمصفوفة الأصلية وتتم هذه العملية بكل سهولة من خلال تبديل أماكن الصفوف بأماكن الأعمدة أو العكس ويمكننا الحصول على المصفوفة المعكوسة ويمكن أن تتم عن طريق القسمة، فإذا قمنا بضرب رقم معين في مقلوبه سنحصل على الواحد الصحيح، فعلى سبيل المثال (5/8) x = 11، فيمكننا أن نقوم بالقسمة لكلا الجانبين على 5/8 ، ولكن من الأسهل أن نقوم بضرب الطرفين في 8/5 فيعتبر الكسر المقلوب 8/5 هو معكوس 5/8 وعندما نقوم بضرب الكسرين في بعضهما البعض سوف نحصل على قيمة الواحد الصحيح وتسمى هذه الحالة هي التطابق فعند ضرب شيء في 1 لا يغير قيمته فمثلا إذا كان لدينا معادلة لمصفوفة مثل AB = C، حيث A وC معطيان فيمكن الحصول على قيمةB، فيمكن الحصول على القيمة من خلال القسمة ولكن القسمة للمصفوفات غير ممكنة.
12-المصفوفة المثلثية العليا
المصفوفة المثلثية العليا هي مصفوفة مربعة تتكون جميع العناصر أسفل القطر من أصفار وباقي العناصر تحتوي على أرقام.
13-المصفوفة المثلثية السفلية
المصفوفة المثلثية السفلية هي مصفوفة مربعة مثل المصفوفة المثلثية العليا ولكن الأصفار للعناصر تكون أعلى القطر.
14-المصفوفة الابتدائية
تعتبر المصفوفة الأولية هي المصفوفة التي يتم إجراء التبديلات عليها من خلال الصفوف أو الأعمدة مثل عمليات الصف الأولية التي يمكن أن تتم على الأعمدة أيضا فتعتبر عمليات التبديل تتم للصفوف والأعمدة للمصفوفة والمصفوفة الأولية تختلف تماما عن مصفوفة الهوية التي تمتلك الرقم واحد في القطر.
تعريف المصفوفات في الحاسب
المصفوفة هي تركيبة من البيانات يتم إنشائها بشكل برمجي في الحاسوب، يمكنها تخزين العديد من العناصر من نفس النوع و كل عنصر يحمل قيمة، يتم حجز مساحة من الذاكرة لتحمل قيمة و مكان كل عنصر بشكل متسلسل، المصفوفة لها سعة ثابتة و لا تتغير خلال وقت التنفيذ لهذا يجب تحديد سعة المصفوفة خلال وقت البرمجة. المصفوفة يمكن أن تحتوي بيانات ببعد واحد أو أكثر و المصفوفة الثنائية البعد يمكن تصورها على أنها مصفوفات داخل اخرى فالبعد الأول يمكن اعتباره المصفوفة الرئيسية أما البعد الثاني فهو مصفوفة داخل البعد الأول وكل عنصر من المصفوفة له حجم خاص به و حسب نوع المصفوفة، السعة الكلية للمصفوفة عبارة عن حجم العنصر مضروب في عدد العناصر .
مقدمة في المصفوفات
-يمثل أول شكل لاستخدام المصفوفات عند حل المعادلات باللغة الصينية ويطلق عليه “تسعة فصول من الفن الرياضي”. ويتضمن أيضًا المبدأ المحدد والذي يمكن إرجاعه إلى ما بين 300 قبل الميلاد و200 بعد الميلاد. وفي عام 1683 نشر عالم الرياضيات الياباني سيكي تاكاكازو ورقة عن المصفوفات. يليه العالم الألماني جوتفريد لايبنيز نشر ورقة بحثية عن المصفوفات عام 1693 ونشر غابرييل كرامر بعد ذلك قواعده الحسابية في عام 1750.
-ركزت نظرية المصفوفة المبكرة على دور المحدد بدلاً من أن تكون مستقلة عن المصفوفة. ولم يظهر مفهوم المصفوفة بشكل مستقل مع آرثر كايلي ونظرية المصفوفة الخاصة به حتى عام 1858.
– نظرية المصفوفة هي فرع من فروع الرياضيات تركز على دراسة المصفوفات وفي الواقع. وتعتبر أحد فروع الجبر الخطي لذلك فهو يغطي بالفعل موضوعات متعلقة بنظرية الرسم البياني والجبر والتوافقيات والإحصاءاتوتمثل المصفوفة مجموعة مستطيلة من الأرقام وفي عام 1848 كما صاغ عالم الرياضيات الإنجليزي جيمس جوزيف سيلفستر مصطلح المصفوفة كاسم لمجموعة من الأرقام المرتبة. وفي عام 1855 اقترح آرثر كايلي مصفوفة لتمثيل العناصر الخطية وتعتبر هذه الفترة بداية نظرية الجبر الخطي والمصفوفة.
– وتعتبر دراسة الفراغات المتجهة في مجالات محددة فرعًا من الجبر الخطي المفيد في نظرية التشفير والذي يؤدي بشكل طبيعي إلى البحث واستخدام المصفوفات في مجالات محددة في نظرية التشفير والوحدة عبارة عن تعميم لفضاء المتجه فيتم التفكير في الأمر على أنه مساحة للناقلات على الحلبة وأدى هذا إلى البحث حول حلقات المصفوفات ولا تعتبر نظرية المصفوفة في هذا المجال فرعًا من فروع الجبر الخطي إلا إذا كانت الحلقة الموضحة متبادلة. والنظرية والنتائج في نظرية كيلي هاملتون مقبولة إذا كانت الحلقة المحددة حقلًا مثاليًا رئيسيًا. فإن شكل سميث الطبيعي يكون متوافقًا ولكن البقية قابلة للتطبيق فقط في حالة مصفوفة ذات معقد أو حقيقية الأعداد.
تعاريف خاصة بالمصفوفات
1-المتّجه:
هو المصفوفة المؤلفة من صفٍ واحدٍ وعمودٍ واحدٍ، حيث أن المصفوفة ذات العمود الواحد يُرمز لها بالشكل Am*1 وتعرف باسم متجه عمودي، بينما المصفوفة المؤلفة من صف واحد يُرمز لها ب A1*n وتعرف باسم متجه صفي.
2-حيّز المصفوفة أو رتبتها أو قياسها:
يعرّف بأنه عدد الأسطر في جداء عدد الأعمدة؛ أي إذا كان لدينا مصفوفة تحتوي على 5 أسطر و 3 أعمدة فإن قياسها أو رتبتها هو 3*5 .
3-معكوس مصفوفة:
هو المعكوس الضربي للمصفوفة بحيث يكون حاصل ضرب المصفوفة في معكوسها يساوي مصفوفة الواحد أي B = In وتدعى المصفوفة B مقلوب A ورمزها A-1 .4
4-منقول مصفوفة:
منقول مصفوفة: هو المَصفوفة الناتجة عن تبديل الأعمدة بالأسطر ويرمز لها AT ومن خواصها أن منقول مجموع مصفوفتين هو مجموع منقول مصفوفتين أي (A+B)T = AT+BT ، وأيضًا منقول حاصل ضرب مصفوفتين هو حاصل ضرب المصفوفتين بشكلٍ معاكسٍ لمنقولهما أي ( A.B)T = BT*AT