جمع المتجهات في الفيزياء جمع وطرح المتجهات في الفيزياء محصلة المتجهات في الفيزياء وسوف نتحدث عن ماهو مفهوم الكميات المتجهة؟ تجدون كل تلك الموضوعات من خلال مقالنا هذا
محتويات المقال
جمع المتجهات في الفيزياء
يمكننا تمثيل المتجهات جبريًّا. في الشكل التالي، يمكن كتابة المتجه ⃑? على الصورة: 2⃑?+3⃑?؛ حيث ⃑? و⃑? هما متجهَا وحدة. متجه الوحدة هو متجه طوله 1، ويشير في اتجاه أحد المحورين. متجه الوحدة ⃑? يشير في اتجاه المحور ?، ومتجه الوحدة ⃑? يشير في اتجاه المحور ?. طول المركِّبة الأفقية للمتجه ⃑? يساوي طول ضلعَي مربعين من مربعات الشبكة، ومن ثَمَّ يمكن وصف مركِّبته الأفقية على الصورة: 2⃑?، أو «2 في متجه الوحدة باتجاه المحور ?». وطول المركِّبة الرأسية للمتجه ⃑? يساوي طول 3 أضلاع من مربعات الشبكة، ومن ثَمَّ يمكن وصف مركِّبته الرأسية على الصورة: 3⃑?، أو «3 في متجه الوحدة باتجاه المحور ?». ولذا يكون المتجه ⃑?=2⃑?+3⃑?.
جمع وطرح المتجهات في الفيزياء
1-طرح المتّجهات
عمليّة الطرح في المتجهات هي نفسها عمليّة الجمع، ولكن بدل جمع متّجهين فإنّه تتمّ إضافة المتجه الأول إلى سالب المتجه الثاني؛ أي إضافة المتجه الثاني بعد عكس اتجاهه.
2-جمع المتجهات
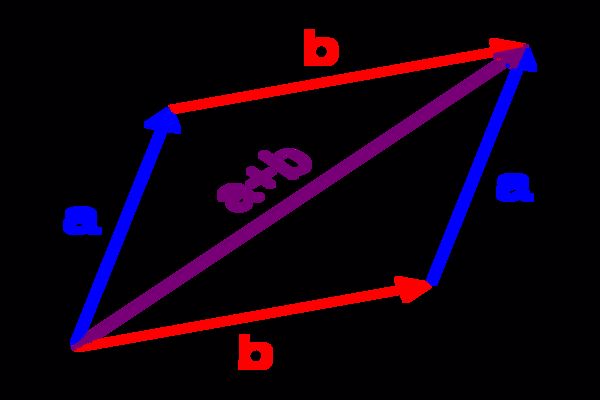
يمكن جمع المتجهات عن طريق جمع مُركّبات المتّجه معاً؛ أي جمع المركبات السينيّة، وجمع المركبات الصاديّة، وجمع المركبات العينيّة كلٌّ على حِدة، أو يمكن جمع المتجهات بطريقة هندسيّة؛ بحيث يوضَع المتجه الأول ثمّ يوضَع ذيل المتجه الثاني على رأس الأول، وهكذا، وفي النهاية يُرسَم سهم من ذيل المتجه الأول إلى رأس الأخير، ويكون حاصل الجمع هو هذا المتجه الأخير الذي تمّ رسمه، وهو ما يُعرَف بالمتجه المُحصّل، ويخضع جمع المتجهات للخاصيّتين التبديليّة والترابطيّة للجمع.
محصلة المتجهات في الفيزياء
عند حركة جسم بين نقطتين او اكثر تتولد إزاحات متعددة لها قيمة واتجاه ولجل إيجاد المحصلة النهائية لإزاحة الجسم الكلية بين النقطة الأولى والنهائية تضاف هذه الإزاحات الى بعضها البعض او أن تطرح هذه الإزاحات من بعضها البعض (إذا كان اتجاهاتها متعاكسة) ولذلك يمكن تقسيم طريقة إيجاد محصلة الإزاحات إلى نوعين
1-إضافة المتجهات (Vector Addition)
عند إضافة متجهين او اكثر إلى بعضها البعض يجب ان تكون هذه الكميات المتجهة من نفس النوع (إزاحات او قوى، مثلاً) وأن تكون ذلك وحدات قياس متماثلة،
2- طرح المتجهات (Subtraction of Vectors)
وتستخدم هذه الطريقة لإيجاد محصلة إزاحتان او اكثر عند تعاكس إحداها الاخرى في الاتجاه أو كلياً. ويمكن الاستفادة من مفهوم المتجه السالب (The Neghative of a Vector) لتغيير عملية طرح المتجهات إلى عملية جمع ثم التعامل معها. ويعرف المتجه السالب على أنه المتجه الذي إذا أضيف إلى المتجه الأصلي ستكون محصلة جمع المتجهين صفراً. فمثلاً إذا أضيف المتجه السالب (-A) إلى المتجه A كانت محصلة جمع المتجهين ستكون صفراً حيث المتجه –A يساوي بالقيمة المتجه A وبعاكسه بالاتجاه وكما يلي:
ماهو مفهوم الكميات المتجهة؟
المتجه في الفيزياء، هو كمية لها مقدار واتجاه، ويتم تمثيله عادةً بواسطة سهم يكون اتجاهه هو نفس اتجاه الكمية ويكون طوله متناسبًا مع حجم الكمية، وعلى الرغم من أن المتجه له مقدار واتجاه، إلا أنه ليس له موضع، أي أنه طالما لم يتغير طوله، فلا يتم تغيير المتجه إذا تم إزاحته بالتوازي مع نفسه. على عكس المتجهات تسمى الكميات العادية التي لها حجم ولكن ليس اتجاهًا كميات قياسية، وعلى سبيل المثال الإزاحة والسرعة والتسارع هي كميات متجهة، في حين أن السرعة (مقدار السرعة) والوقت والكتلة هي كميات قياسية. للتأهل كمتجه، يجب أن تمتثل الكمية التي لها حجم واتجاه أيضًا لقواعد معينة للجمع، واحدة من هذه هي إضافة ناقلات، مكتوبة بشكل رمزي كـ A + B = C (يتم كتابة المتجهات بشكل تقليدي كأحرف غامقة)، وهندسيًا يمكن تصور مجموع المتجه عن طريق وضع ذيل المتجه B على رأس المتجه A ورسم المتجه C بدءًا من ذيل A وينتهي عند رأس B – بحيث يكمل المثلث. إذا كانت A و B و C متجهات، فيجب أن يكون من الممكن إجراء نفس العملية وتحقيق نفس النتيجة (C) بترتيب عكسي، B + A = C، وتمتلك الكميات مثل الإزاحة والسرعة هذه الخاصية (قانون التبادل)، ولكن هناك كميات (على سبيل المثال، دوران محدود في الفضاء) لا تكون متجهة، وبالتالي فهي ليست نواقل.