حل التعبير عن المتجهات في الفضاء جبريا وخصائص المتجهات وتعريف المتجهات وتحليل المتجهات، هذا ما سوف نتعرف عليه فيما يلي.
محتويات المقال
حل التعبير عن المتجهات في الفضاء جبريا
خصائص المتجهات في الفضاء تشبه خصائص العمليات على المتجهات في الفضاء تلك الخاصة بالعمليات في المستوى، حيث يمكن تحديد التساوي والجمع (الطرح، وحاصل الضرب القياسي وطول المتجه بدلالة المركبات أو i j k للمتجه، فإذا كان a) = و ,az a و b = ( b + b b وأي عدد حقيقي n، فإن . a = b فقط
خصائص المتجهات
1-جمع المتجهات
تقبل المتجهات الجمع و يمكننا جمع المتجهات من خلال جمع مركبات المتجه مع بعضها البعض ، حيث نقوم بجمع المركب السيني و المركب الصادي و المركب العيني مع بعضها كل على حدة ، كما انه يوجد طريقة هندسية أيضا لجمع المتجهات و ذلك من خلال تمثيل المتجه الأول ثم نقوم بوضع ذيل المتجه الثاني على رأس المتجه الأول و هكذا و في النهاية نقوم برسم سهم من ذيل المتجه الأول إلى رأس المتجه الثاني ، و هذا المتجه الأخير الذي قمنا برسمه هو حاصل عملية الجمع ويسمى المتجه المحصل ، و يتميز جمع المتجهات بخصائص الجمع التبديلية و الترابطية .
2-تساوي المتجهات
و إذا وجد متجهان لهما نفس الطول و المقدار و يكون متجهين إلى نفس الاتجاه أي يشيران إلى اتجاه واحد فإن هذان المتجهان يكونون في هذه الحالة متساويين ، و مثالا على تساوي المتجهات يمكننا القول أن هناك متجهين يشيران إلى الجنوب و مقدار كل متجه منهما 5 إذن يمكننا القول إن هذان المتجهان متساويان ، أما لو كان لأحد المتجهات مقدار مختلف عن الآخر أو انه يشير إلى اتجاه مختلف عن الآخر فإن هذين المتجهين لن يكونا متساويين .
3-ضرب المتجهات
المتجهات كميات تقبل الضرب كذلك ، حيث يمكننا ان نقوم بضرب متجه ما بكمية قياسية ، و عملية ضرب متجه بكمية قياسية هي عبارة عن تغيير في طول المتجه أي أننا في عملية الضرب نقوم بتغيير مقدار المتجه و لكن اتجاهه لن يتغير لو تم ضربه في أي رقم و اما عن ضرب المتجهات في بعضها البعض فإنه يوجد نوعين من ضرب المتجهات حيث أنه لو قمنا بضرب متجهين من خلال الضرب النقطي فإن الناتج من هذه العملية سوف يكون عبارة عن كمية قياسية و لذلك فإن هذا النوع من الضرب يعرف الضرب القياسي ، أما النوع الثاني من ضرب المتجهات فإنه يسمى الضرب الاتجاهي و فيه تقوم بضرب المتجهين ضربا تقاطعوا والناتج هنا يكون متجها جديد عمودي على المتجهين الذين قمنا بضربهما .
4-طرح المتجهات
المتجهات تقبل الطرح كذلك ، و كما فعلنا في عملية جمع المتجهات يمكننا العمل في الطرح ، و لكن مع ملاحظة انه عملية الطرح هى نفسها عملية الجمع و لكن لن نقوم بعملية جمع متجهين كما فعلنا في عملية جمع المتجهات و لكن في عملية الطرح سوف نقوم بإضافة المتجه الأول إلى سالب المتجه الثاني ، أي أننا نقوم بإضافة المتجه الثاني و لكن بعدما نقوم بعكس اتجاه هذا المتجه .
بحث رياضيات عن المتجهات
5-متجه الوحدة
و يمكننا تعريف متجه الوحدة على أنه متجه يبلغ مقداره واحد و يكون عديم الأبعاد ، و أما عن اتجاه متجه الوحدة فإنه يعبر عن اتجاه كل مركب في مركبات المتجه ، و يختلف متجه الوحدة بحسب اختلاف النظام الاحداثي الذي نقوم باستخدامه ، حيث انه لو كانت هناك زاوية وجوده بين المحور السيني و المتجه فإن مقدار المركب السيني يكون متساوي مع طول هذا المتجه و يكون مضروب في جيب تمام هذه الزاوية ، كما أن المركب الصادي سوف يكون متساوي مع طول هذا المتجه و مضروب في جيب تمام هذه الزاوية .
6-المتجه السالب
لو كان عندنا المتجه ” أ ” فإن المتجه السالب من هذا المتجه هو المتجه الذي يكون ناتج جمعه مع المتجه ” أ ” صفر ، فلو قمنا بجمع متجه ما مع متجه آخر ووجدنا أن ناتج هذه العملية هو صفر فإن هذا المتجه هو المتجه السالب للمتجه الذي قمنا بجمعه معه ، و المتجه السالب يكون له نفس مقدار مثيله الموجب و لكن ف اتجاه معاكس له حيث يكون الفرق بينهما 180 درجة .
تعريف المتجهات
المتجهات هي تمثيلات هندسية للحجم والاتجاه والتي يتم تمثيلها غالبًا بأسهم مستقيمة ، تبدأ من نقطة واحدة على محور إحداثيات وتنتهي عند نقطة مختلفة ، جميع المتجهات لها طول ، يُطلق عليه المقدار ، والذي يمثل نوعًا ما من الفائدة بحيث يمكن مقارنة المتجه مع متجه آخر ، المتجهات كونها سهام ، لها أيضًا اتجاه ، هذا ما يميزهم عن العددية ، وهي مجرد أرقام بدون اتجاه ، وتستخدم في العديد من التطبيقات مما يجعل اهمية المتجهات في حياتنا كبيرة.
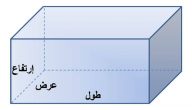
يتم تعريف المتجه من خلال حجمه واتجاهه فيما يتعلق بمجموعة من الإحداثيات ، غالبًا ما يكون مفيدًا في تحليل المتجهات لتقسيمها إلى الأجزاء المكونة لها ، بالنسبة للمتجهات ثنائية الأبعاد ، تكون هذه المكونات أفقية ورأسية ، بالنسبة للمتجهات ثلاثية الأبعاد ، يكون عنصر المقدار هو نفسه ، ولكن يتم التعبير عن مكون الاتجاه بدلالة xx و yy و zz.
وبالتالي من حيث التعريف ، فإن المتجه هو كمية تتميز بالحجم والاتجاه ، ومن أشهر الأمثلة على ذلك هي القوة ، السرعة ، والوزن ، وتعتبر القوة متجه لأن القوة هي مقدار الشدة أو القوة المطبقة في اتجاه ما ، والسرعة هي المتجه حيث تكون سرعته هي المقدار الذي يتحرك فيه كائن في مسار معين.
تحليل المتجهات
1-هو فرع من الرياضيات يتعامل مع الكميات ذات الحجم والاتجاه، ويمكن تحديد بعض الكميات الفيزيائية والهندسية، المسماة بالكميات، بشكل كامل من خلال تحديد حجمها في وحدات قياس مناسبة، وهكذا يمكن التعبير عن الكتلة بالجرام، ودرجة الحرارة بالدرجات على مقياس ما، والوقت بالثواني. يمكن تمثيل المقاييس بيانياً بنقاط على بعض المقاييس الرقمية مثل الساعة أو مقياس الحرارة، وهناك أيضًا كميات، تسمى المتجهات تتطلب تحديد الاتجاه بالإضافة إلى الحجم، تعد السرعة والقوة والإزاحة أمثلة على المتجهات، ويمكن تمثيل كمية المتجه بيانياً بواسطة مقطع خط موجه، ويُرمز إليه بسهم يشير في اتجاه كمية المتجه، ويمثل طول المقطع حجم المتجه.
2-النموذج الأولي للمتجه هو جزء من الخط الموجه AB والذي يمكن اعتباره يمثل إزاحة الجسيم من موضعه الأولي A إلى موضع جديد B، ويعبر عنه بأحرف غامقة، وبالتالي يمكن الإشارة إلى المتجه AB بـ a وطوله (أو حجمه) بواسطة|a| في العديد من المسائل، يكون موقع النقطة الأولية للمتجه غير مادي، لذلك يُعتبر المتجهان متساويين إذا كان لهما نفس الطول والاتجاه. يُشار إلى المساواة بين المتجهين أ و ب بواسطة التدوين الرمزي المعتاد أ = ب، وتقترح الهندسة التعريفات المفيدة للعمليات الجبرية الأولية على المتجهات، وبالتالي إذا كان AB = a يمثل إزاحة لجسيم من A إلى B، وبالتالي يتم نقل الجسيم إلى الموضع C، بحيث يكون BC = b، فمن الواضح أن الإزاحة من A إلى C يمكن تحقيقها بواسطة إزاحة واحدة AC = c. وبالتالي، فمن المنطقي أن تكتب a+b=c. هذا البناء لمجموع، c ، لـ a و b ينتج نفس النتيجة مثل قانون متوازي الأضلاع، حيث يتم إعطاء الناتج c بواسطة القطر AC لمتوازي الأضلاع المبني على المتجهين AB و AD كأضلاع، ونظرًا لأن موقع النقطة الأولية B للمتجه BC = b غير مادي، فإنه يتبع ذلك BC = AD و أن AD + DC = AC، بحيث يكون القانون التبادلي