قواعد المستطيل

قواعد المستطيل نتعرف عليها بشكل تفصيلي من خلال مقالنا هذا كما نذكر لكم قانون طول المستطيل هذا بالإضاغفة إلى قواعد المستطيل والمربع والمثلث وقوانين المساحة والحجم والمحيط للأشكال الهندسية والختام معلومات مختلفة حول المستطيل.

قواعد المستطيل

أولا قانون حساب محيط المستطيل
يتمّ حِساب محيط المستطيل حسب ما هو معلوم منه كالتالي:
1-عندما تكون علي علم بالطول والقطر، أو طول القطر والعرض: محيط المستطيل
= 2× (الطول أو العرض+ (مربع القطر-مربع الطول أو مربع العرض) √)، وبالرموز: ح= 2×(أ+(ق²-أ²) √)، أو ح= 2×(ب+(ق²-ب²) √)؛ حيث:
أ: طول قطر المستطيل.
ب: محيط المستطيل.
ح: عرض المستطيل.
ق: طول المستطيل.
2-عندما تكون علي علم بطوله وعرضه يكون محيط المستطيل
=طول الضلع الأول+ طول الضلع الثاني+ طول الضلع الثالث+ طول الضلع الرابع،وذلك بسبب أن كل ضلعين متساويان بالنسبة للمستطيل متساويان في الطول، فمن الممكن أن يكتب القانون بهذا الشكل: محيط المستطيل= 2×الطول+2×العرض، وبالرموز: ح=2×أ+2×ب، حيث:
أ: عرض المستطيل.
ب: طول المستطيل.
3-عندما تكون علي علم بالطول والعرض، أو الطول والمساحة يكون محيط المستطيل
=(2×مساحة المستطيل+2×مربع الطول أو مربع العرض) /الطول أو العرض، وبالرموز: ح=((2×م+2×أ²) /أ أو ح=((2×م+2×ب²) /ب؛ حيث:
أ: عرض المستطيل.
ب: طول المستطيل.
ح: مساحة المستطيل.
م: محيط المستطيل.
حساب مساحة المستطيل
يتمّ حِساب مساحة المستطيل حسب ما هو معلوم منه كالتالي:
1-القانون الأول:
إيجاد مساحة المستطيل إذا عُرِفَ مُحيط المستطيل وأحد أبعاده:
مساحة المستطيل = (المحيط ×الطول- 2× مربع الطول)/2 مساحة المستطيل = (المحيط×العرض-2× مربع العرض)/2
2-القانون الثاني:
إيجاد مساحة المستطيل إذا عُرِفَت كلٌّ من أبعاده، وهما الطول والعرض:
مساحة المستطيل = ( طول الضلع الأول (الطول) × طول الضلع الثاني (العرض))
3-القانون الثالث:
إيجاد مساحة المستطيل إذا عُرِفَ طول أحد أبعاده، وطول قطره:
مساحة المستطيل= الطول×(مربّع القطر- مربع الطول)^(1/2) مساحة المستطيل = العرض×(مربع القطر- مربع العرض)^(1/2)

قانون طول المستطيل

يمكننا حساب طول المستطيل في عدة حالات وهي:
1-بمعرفة عرضه و محيطه
سوف نستخدم القانون التالي :
طول المستطيل = ( محيط المستطيل – (2 × العرض) ) ÷ 2
2-بمعرفة عرضه ومساحته
القانون :طول المستطيل = مساحة المستطيل ÷ العرض
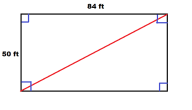
يعمل القطران على تقسيم المستطيل إلى مثلثيْن متطابقين بهما زاوية قائمة.
في كل مثلث يكون القطر هر الوتر وتبعاً لـ نظرية فيثاغورس يمكن حساب طول قطر المستطيل كالآتي:
طول المستطيل = الجذر التربيعي للناتج من (الطول²+العرض²).
الرموز: ق=(أ²+ب²)√.
تشير الرموز إلى:
ق: قطر المستطيل.
أ: طول المستطيل.
ب: عرض المستطيل.
3-بمعرفة عرض المستطيل و احد اقطاره.
القانون= الجذر التربيعي للقيمة (مربع المساحة + أحد الأبعاد (الطول أو العرض)4) /الطول أو العرض.
الرموز: ق= (م²+أ4)√/أ، أو ق= (م²+ب4)√/ب.
تشير الرموز إلى:
ق: قطر المستطيل.
أ: طول المستطيل.
ب: عرض المستطيل.
م: مساحة المستطيل.

قواعد المستطيل والمربع والمثلث

1-المربع:
مساحة المربع = طول الضلع في نفسه
محيط المربع = 4× طول الضلع
2-المستطيل:
مساحة المستطيل = الطول× العرض
محيط المستطيل = 2(الطول + العرض)
3-المثلث:
مساحة المثلث = نصف طول القاعدة × الارتفاع
= نصف حاصل ضرب الضلعين × جيب الزاوية المحصورة بينهما
محيط المثلث = مجموع أطوال اضلاعه

قوانين المساحة والحجم والمحيط للأشكال الهندسية

1-المنشور القائم
المساحة الجانبية للمنشور القائم = محيط القاعدة × ارتفاع المنشور
المساحة الكلية للمنشور القائم =مساحته الجانبية + ( 2× مساحة القاعدة )
حجم المنشور القائم = مساحة قاعدته × ارتفاعه
2-الدائرة:
مساحة الدائرة = ط نق 2
محيط الدائرة = 2 ط نق ( مشتقة المساحة)
3-متوازي الاضلاع:
مساحة متوازي الاضلاع = القاعدة × الارتفاع
محيط متوازي الاضلاع = 2× مجموع الضلعين المتجاورين
4-الكرة:
المساحة = 4 ط نق2
الحجم = 3/4 ط نق3
5-متوازي المستطيلات:
المساحة الكلية = مجموع مساحات الأوجه الستة
المساحة الجانبية = محيط القاعدة × الارتفاع
الحجم = مساحة القاعدة × الارتفاع
6-المعين
مساحة المعين = القاعدة × الارتفاع
مساحة المعين = 1/2 × حاصل ضرب القطرين = 1/2 × القطر × القطر
محيط المعين = 4 × طول الضلع
7-المكعب:
المساحة الجانبية = محيط القاعدة × الارتفاع = 2 ط نق ع
المساحة الكلية = المساحة الجانبية + ضعف مساحة القاعدة
الحجم = مساحة القاعدة × الارتفاع
8-المخروط القائم:
الحجم = 3/1 مساحة القاعدة × الارتفاع
= 3/1 ط نق 2 × ع

معلومات مختلفة حول المستطيل

مفهوم المستطيل:
يُعرف المستطيل بأنه من أحد أهم الأشكال الهندسية ذات الاستخدامات الواسهة المهمة، والذي يحتوي على أربعة أضلاع، وأربعة زوايا وكل زاوية فيه تساوي 90 درجة، فمحصلة مجموع قياسات زواياه تساوي 360 درجة، ويتميز بالعديد من الخصائص المهمة التي تجعله أكثراستخداماً وشهرة.
خصائص المستطيل:
1-يتكون من أربعة أضلاع، كل ضلعين فيه متقابلين متساويين ومتوازيين.
2-فيه أربعة زوايا متساوية و قوائم ( كل زاوية من زواياه تساوي 90 درجة).
3-قطراه متساويان وينصف كل منهما الآخر.
4-هو شكل من الأشكال الهندسية، ويعتبر شكل ثنائي الأبعاد ( الطول والعرض ).
كيف نثبت بأن الشكل مستطيل؟
من خلال التأكد من خواص المستطيل إذا كان الشكل على هيئة ثنائي الأبعاد، وتتكون أضلاعه من أربعة أضلاع، زواياه الأربع جميعها 90، فيه كل ضلعين متقابلين متوازيين وكل ضلعين متقابلين متساويين، تعتبر جميع أقطاره متساوية وكل من ينصف الآخر، إذا توفرت تلك الخصائص فهو مستطيل.
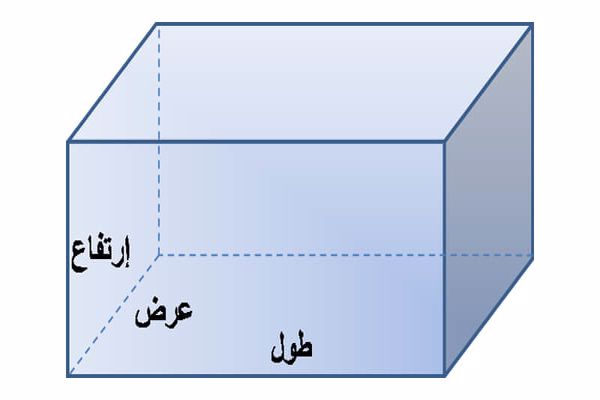
مفهوم متوازي المستطيلات
متوازي المستطيلات هو عبارة عن شكل هندسي ثلاثي الأبعاد على هيئة مجسم ثلاثي الأبعاد (طول وعرض وارتفاع، وهو شكل يشبه الصندوق على شكل مستطيل، ويتميز متوازي المستطيلات بمجموعة من الخصائص تميزه عن غيره من المجسمات الأخرى.
خصائص متوازي المستطيلات:
1-يحتوي على أربعة جوانب مستطيلة الشكل وقاعدتين متوازيتين ومتطابقتين.
2-متوازي المستطيلات هو مجسم ثلاثي الأبعاد (الطول والعرض والارتفاع).
3-له ثمانية زوايا وجميعها قوائم.
4-يتشابه مع المثلث ولكن الاختلاف يكون في أطوال الأضلاع.
5-نستطيع إيجاد مساحة متوازي المستطيلات من خلال ايجاد المساحة الجانبية = محيط القاعدة × الارتفاع، المساحة الكلية= المساحة الجانبية +مساحة القاعدتين.
6-له ستة أوجه كل منها على شكل مستطيل
7-يسمى متوازي المستطيلات بذلك الاسم، لأنه يتكون من ستة أوجه مستطيلة كل شكل يوازي الشكل الذي يقابله.
كيف نقوم ببرهان الشكل الرباعي هل هو متوازي مستطيلات؟
من المعروف أن الشكل الرباعي يكون على هيئة ثنائي الأبعاد بما معناه (طول وعرض )، وأضلاعه هي 4 فقط، بالنسبة لمتوازي المستطيلات يكون على شكل ثلاثي الأبعاد إذن فهو يعتبرمجسم، له عدة وجوه و12 ضلع و ليس 4 أضلاع، تكون تلك الوجوه عبارة عن أشكال هندسية ثنائية الأبعاد بالتالي تكون مستطيلة الشكل.